
 已知:如图,在直角△ABC中,∠ACB=90°,∠CAB=30°,P为形内一点,∠BPC=120°,若BP=3,则△PAB的面积为( )
已知:如图,在直角△ABC中,∠ACB=90°,∠CAB=30°,P为形内一点,∠BPC=120°,若BP=3,则△PAB的面积为( )| A. | 9 | B. | 4$\sqrt{3}$ | C. | 3$\sqrt{3}$ | D. | $\frac{9\sqrt{3}}{2}$ |
分析 如图,作△BPC的外接圆⊙O,交AC的延长线于D,连接BD、PD.利用切线的性质和圆内接四边形的内对角互补得到∠BDA=180°-∠BPC=60°,所以∠ABD=180°-∠BAC-∠BDA=90°,即AB是⊙O的切线.设∠ABP=∠BDP=α.通过解直角△ABD、△BPD求得AB、AP的长度,然后由三角形的面积公式S=$\frac{1}{2}$absinC进行计算即可.
解答 解:如图,作△BPC的外接圆⊙O,交AC的延长线于D,连接BD、PD.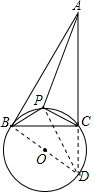
∵∠ACB=90°,
∴∠BCD=90°,
∴BD是⊙O的直径.
∵四边形BDCP是圆内接四边形,
∴∠BDA=180°-∠BPC=60°,
∴∠ABD=180°-∠BAC-∠BDA=180°-30°-60°=90°,则AB是⊙O的切线.
设∠ABP=∠BDP=α.
在直角△ABD中,AB=BD•tan∠BDA=$\sqrt{3}$BD,
在直角△BPD中,BP=BD•sin∠BDP=BDsinα=3,
则△PAB的面积是:$\frac{1}{2}$AB•BPsin∠ABP=$\frac{1}{2}$×$\sqrt{3}$BD×3sinα=$\frac{3\sqrt{3}}{2}$×3=$\frac{9\sqrt{3}}{2}$.
故选:D.
点评 本题考查了圆的综合题.其中涉及到了圆周角定理,圆内接四边形的性质,解直角三角形以及三角形的面积计算.此题的难点是作出△BPC的外接圆⊙O.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:填空题
 如图,为了使电线杆稳固的垂直于地面,两侧常用拉紧的钢丝绳索固定,由于钢丝绳的交点E在电线杆的上三分之一处,所以知道BE的高度就可以知道电线杆AB的高度了.要想得到BE的高度,需要测量出一些数据,然后通过计算得出.
如图,为了使电线杆稳固的垂直于地面,两侧常用拉紧的钢丝绳索固定,由于钢丝绳的交点E在电线杆的上三分之一处,所以知道BE的高度就可以知道电线杆AB的高度了.要想得到BE的高度,需要测量出一些数据,然后通过计算得出.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a、b都是负数 | B. | b是正数,a是负数 | C. | a、b都是正数 | D. | a是正数,b是负数 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,用三角尺可按下面方法画角平分线:在已知的∠AOB 的两边上分别取点M、N,使OM=ON,再分别过点M、N作OA、OB的垂线,交点为P,画射线OP.可证得△POM≌△PON,OP平分∠AOB.以上依画法证明△POM≌△PON根据的是( )
如图,用三角尺可按下面方法画角平分线:在已知的∠AOB 的两边上分别取点M、N,使OM=ON,再分别过点M、N作OA、OB的垂线,交点为P,画射线OP.可证得△POM≌△PON,OP平分∠AOB.以上依画法证明△POM≌△PON根据的是( )| A. | SSS | B. | HL | C. | AAS | D. | SAS |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
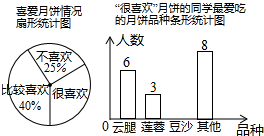 中秋佳节我国有赏月和吃月饼的传统,某校数学兴趣小组为了了解本校学生喜爱月饼的情况,随机抽取了60名同学进行问卷调查,经过统计后绘制了两幅尚不完整的统计图.(注:参与问卷调查的每一位同学在任何一种分类统计中只有一种选择)
中秋佳节我国有赏月和吃月饼的传统,某校数学兴趣小组为了了解本校学生喜爱月饼的情况,随机抽取了60名同学进行问卷调查,经过统计后绘制了两幅尚不完整的统计图.(注:参与问卷调查的每一位同学在任何一种分类统计中只有一种选择)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com