
【题目】宜兴紧靠太湖,所产百合有“太湖人参”之美誉,今年百合上市后,甲、乙两超市分别用12000元以相同的进价购进质量相同的百合,甲超市销售方案是:将百合按分类包装销售,其中挑出优质的百合400千克,以进价的2倍价格销售,剩下的百合以高于进价10%销售.乙超市的销售方案是:不将百合分类,直接包装销售,价格按甲超市分类销售的两种百合售价的平均数定价.若两超市将百合全部售完,其中甲超市获利8400元(其它成本不计).问:
(1)百合进价为每千克多少元?
(2)乙超市获利多少元?并比较哪种销售方式更合算.
【答案】(1)百合进价为每千克20元;(2)8400元,两种销售方式获利一样多.
【解析】
试题分析:(1)设百合进价为每千克x元,根据甲超市获利8400元列出分式方程,求出方程(2)根据(1)求出甲乙两超市购进百合得质量数,求出甲超市分类销售的两种百合售价的平均数定价,即为乙超市的定价,进而求出乙超市的利润,即可做出判断.
试题解析:(1)设百合进价为每千克x元,
根据题意得:400×(2x-x)+(![]() -400)×10%x=8400,
-400)×10%x=8400,
解得:x=20,
经检验x=20是分式方程的解,且符合题意,
则百合进价为每千克20元;
(2)甲乙两超市购进百合的质量数为![]() =600(千克),
=600(千克),
根据(1)得:甲超市平均定价为2×20×![]() +20×(1+10%)×
+20×(1+10%)×![]() =34(元/千克),即乙超市售价为34元/千克,
=34(元/千克),即乙超市售价为34元/千克,
乙超市获利为600×(34-20)=8400(元),则两种销售方式获利一样多.


科目:初中数学 来源: 题型:
【题目】在正方形![]() 中,
中,![]() 是
是![]() 上的一动点,连接
上的一动点,连接![]() ,分别过点
,分别过点![]() 作
作![]() ,垂足为
,垂足为![]() .
.
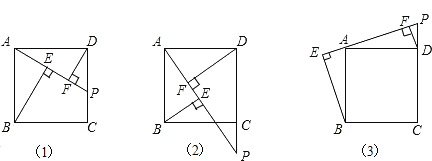
(1)求证:![]() ;
;
(2)如图(2),若点![]() 是
是![]() 的延长线上的一个动点,请探索
的延长线上的一个动点,请探索![]() 三条线段之间的数量关系?并说明理由;
三条线段之间的数量关系?并说明理由;
(3)如图(3),若点![]() 是
是![]() 的延长线上的一个动点,请探索
的延长线上的一个动点,请探索![]() 三条线之间的数量关系?(直接写出结论,不需说明理由)
三条线之间的数量关系?(直接写出结论,不需说明理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】体育文化用品商店购进篮球和排球共20个,进价和售价如表,全部销售完后共获利润260元.
篮球 | 排球 | |
进价(元/个) | 80 | 50 |
售价(元/个) | 95 | 60 |
(1)购进篮球和排球各多少个?
(2)销售6个排球的利润与销售几个篮球的利润相等?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图①、②,解答下面各题:
(1)图①中,∠AOB=55°,点P在∠AOB内部,过点P作PE⊥OA,PF⊥OB,垂足分别为E、F,求∠EPF的度数.
(2)图②中,点P在∠AOB外部,过点P作PE⊥OA,PF⊥OB,垂足分别为E、F,那么∠P与∠O有什么关系?为什么?
(3)通过上面这两道题,你能说出如果一个角的两边分别垂直于另一个角的两边,则这两个角是什么关系?
(4)如果一个角的两边分别平行于另一个角的两边,则这两个角是什么关系?(请画图说明结果,不需要过程)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各式由左边到右边的变形中,属于分解因式的是( )
A. a(x+y)=ax+ay B. x2-4x+4=x(x-4)+4
C. 10x2-5x=5x(2x-1) D. x2-16+6x=(x+4)(x-4)+6x
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com