
【题目】在正方形![]() 中,
中,![]() 是
是![]() 上的一动点,连接
上的一动点,连接![]() ,分别过点
,分别过点![]() 作
作![]() ,垂足为
,垂足为![]() .
.
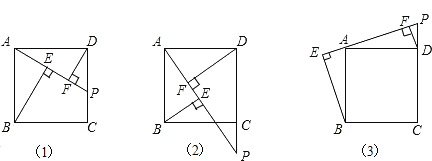
(1)求证:![]() ;
;
(2)如图(2),若点![]() 是
是![]() 的延长线上的一个动点,请探索
的延长线上的一个动点,请探索![]() 三条线段之间的数量关系?并说明理由;
三条线段之间的数量关系?并说明理由;
(3)如图(3),若点![]() 是
是![]() 的延长线上的一个动点,请探索
的延长线上的一个动点,请探索![]() 三条线之间的数量关系?(直接写出结论,不需说明理由)
三条线之间的数量关系?(直接写出结论,不需说明理由)
【答案】(1)BE=EF+DF;(2)DF=EF+BE;(3)EF=BE+DF.
【解析】
试题解析:(1)根据正方形的性质可知证出△ABE≌△DAF,根据全等三角形的性质:全等三角形对应边相等可得:BE=AF,AE=DF,得出BE=EF+DF;
(2)同(1)的证法相同,先证明△ABE≌△DAF,利用全等三角形的性质可得:BE=AF,BE=DF,再根据等量代换可得出图(2)中DF=EF+BE;
(3)同(1)的证法相同,可得出图(3)中EF=EB+FD.
试题解析:(1)BE=EF+DF,
证明:∵BE⊥PA,DF⊥PA,
∴∠BEA=∠AFD=90°,
∵四边形ABCD是正方形,
∴AB=AD,∠BAD=90°,
∴∠BAE+∠DAF=∠ADF+∠DAF=90°,
∴∠BAE=∠ADF,
在△BAE和△ADF中
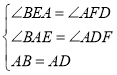 ,
,
∴△BAE≌△ADF(AAS),
∴BE=AF,AE=DF,
∵AF-AE=EF,
∴BE-DF=EF.
(2)DF=BE+EF,
证明:∵四边形ABCD是正方形,
∴AB=AD,∠BAE+∠DAF=90°,
∵BE⊥PA、DF⊥PA,
∴∠AEB=∠DFA=90°,
∴∠BAE+∠ABE=90°,
∴∠ABE=∠DAF,
在△ABE和△DAF中,
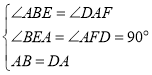 ,
,
∴△ABE≌△DAF(AAS),
∴BE=AF,AE=DF,
∵AE=AF+EF,
∴DF=EB+EF.
(3)EF=BE+DF.
证明:∵四边形ABCD是正方形,
∴AB=AD,∠BAD=90°,
∴∠1+∠3=90°,
∵BE⊥PA、DF⊥PA,
∴∠AEB=∠DFA=90°,
∴∠2+∠3=90°,
∴∠1=∠2,
在△ABE和△DAF中,
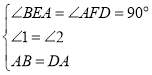 ,
,
∴△ABE≌△DAF(AAS),
∴BE=AF,AE=DF(全等三角形对应边相等),
∵EF=AF+AE,
∴EF=EB+FD(等量代换).



 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】某校九年级(1)班所有学生参加![]() 年初中毕业生升学体育测试,根据测试评分标准,将他们的成绩进行统计后分为
年初中毕业生升学体育测试,根据测试评分标准,将他们的成绩进行统计后分为![]() 、
、![]() 、
、![]() 、
、![]() 四等,并绘制成如图所示的条形统计图和扇形统计图(未完成),请结合图中所给信息解答下列问题:
四等,并绘制成如图所示的条形统计图和扇形统计图(未完成),请结合图中所给信息解答下列问题:
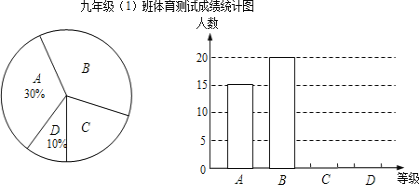
(1)九年级(1)班参加体育测试的学生有 人;
(2)将条形统计图补充完整;
(3)在扇形统计图中,等级![]() 部分所占的百分比是 ,等级
部分所占的百分比是 ,等级![]() 对应的圆心角的度数为 ;
对应的圆心角的度数为 ;
(4)若该校九年级学生共有850人参加体育测试,估计达到![]() 级和
级和![]() 级的学生共有 人.
级的学生共有 人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于任意三角形的高,下列说法不正确的是( )
A. 直角三角形只有一条高
B. 锐角三角形有三条高
C. 任意三角形都有三条高
D. 钝角三角形有两条高在三角形的外部
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(m,1)与点B(5,n)关于原点对称,则m和n的值为
A. m=5,n=-1 B. m=-5,n=1 C. m=-1,n=-5 D. m=-5,n=-1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】宜兴紧靠太湖,所产百合有“太湖人参”之美誉,今年百合上市后,甲、乙两超市分别用12000元以相同的进价购进质量相同的百合,甲超市销售方案是:将百合按分类包装销售,其中挑出优质的百合400千克,以进价的2倍价格销售,剩下的百合以高于进价10%销售.乙超市的销售方案是:不将百合分类,直接包装销售,价格按甲超市分类销售的两种百合售价的平均数定价.若两超市将百合全部售完,其中甲超市获利8400元(其它成本不计).问:
(1)百合进价为每千克多少元?
(2)乙超市获利多少元?并比较哪种销售方式更合算.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com