
【题目】如图,在平面直角坐标系中,矩形OABC的边OA,OC分别在x轴、y轴上,点B坐标为(4,t)(t>0),二次函数y=x2+bx(b<0)的图象经过点B,顶点为点D.
(1)当t=12时,顶点D到x轴的距离等于;
(2)点E是二次函数y=x2+bx(b<0)的图象与x轴的一个公共点(点E与点O不重合),求OEEA的最大值及取得最大值时的二次函数表达式;
(3)矩形OABC的对角线OB、AC交于点F,直线l平行于x轴,交二次函数y=x2+bx(b<0)的图象于点M、N,连接DM、DN,当△DMN≌△FOC时,求t的值.
【答案】
(1)![]()
(2)解:将y=0代入抛物线的解析式得:x2+bx=0,解得x=0或x=﹣b,
∵OA=4,
∴AE=4﹣(﹣b)=4+b.
∴OEAE=﹣b(4+b)=﹣b2﹣4b=﹣(b+2)2+4,
∴OEAE的最大值为4,此时b的值为﹣2,
∴抛物线的表达式为y=x2﹣2x.
(3)解:过D作DG⊥MN,垂足为G,过点F作FH⊥CO,垂足为H.
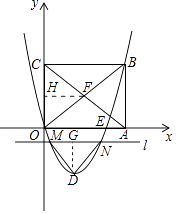
∵△DMN≌△FOC,
∴MN=CO=t,DG=FH=2.
∵D(﹣ ![]() ,﹣
,﹣ ![]() ),
),
∴N(﹣ ![]() +
+ ![]() ,﹣
,﹣ ![]() +2),即(
+2),即( ![]() ,
, ![]() ).
).
把点N和坐标代入抛物线的解析式得: ![]() =(
=( ![]() )2+b(
)2+b( ![]() ),
),
解得:t=±2 ![]() .
.
∵t>0,
∴t=2 ![]() .
.
【解析】(1)当t=12时,B(4,12).
将点B的坐标代入抛物线的解析式得:16+4b=12,解得:b=﹣1,
∴抛物线的解析式y=x2﹣x.
∴y=(x﹣ ![]() )2﹣
)2﹣ ![]() .
.
∴D( ![]() ,
, ![]() ).
).
∴顶点D与x轴的距离为 ![]() .
.
所以答案是: ![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦CD⊥AB于H,G为⊙O上一点,AG交CD于K,E为CD延长线上一点,且EK=EG,EG的延长线交AB的延长线于F. 
(1)求证:EF为⊙O的切线;
(2)若DK=2HK=AK,CH= ![]() ,求图中阴影部分的面积S.
,求图中阴影部分的面积S.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一副扑克牌中取牌面花色分别为黑桃、红心、方块各一张,洗匀后正面朝下放在桌面上.
(1)从这三张牌中随机抽取一张牌,抽到牌面花色为红心的概率是多少?
(2)小王和小李玩摸牌游戏,游戏规则如下:先由小王随机抽出一张牌,记下牌面花色后放回,洗匀后正面朝下,再由小李随机抽出一张牌,记下牌面花色.当两张牌的花色相同时,小王赢;当两张牌面的花色不相同时,小李赢.请你利用树状图或列表法分析该游戏规则对双方是否公平?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
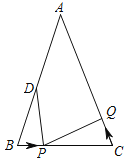
【题目】如图,已知△ABC中,AB=AC=12cm,∠B=∠C,BC=8cm,点D为AB的中点.
(1)如果点P在线段BC上以2cm/s的速度由点B向点C运动,同时,点Q在线段CA上由点C向点A运动.
①若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPD与△CQP是否全等,请说明理由;
②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿△ABC三边运动,则经过多少秒后,点P与点Q第一次在△ABC的哪条边上相遇?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是2019年4月份的日历,现用一长方形在日历表中任意框出4个数(如图2),下列表示a,b,c,d之间关系的式子中不正确的是( )

A. a﹣d=b﹣cB. a+c+2=b+dC. a+b+14=c+dD. a+d=b+c
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的半径为5,弦AB长为8,过AB的中点E有一动弦CD(点C只在弦AB所对的劣弧上运动,且不与A、B重合),设CE=x,ED=y,下列图象中能够表示y与x之间函数关系的是( )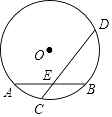
A.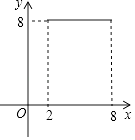
B.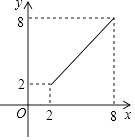
C.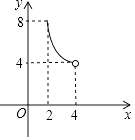
D.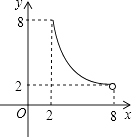
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD中,AE平分∠BAD,交BC于E,DE⊥AE,下列结论::①DE平分∠ADC;②E是BC的中点;③AD=2CD;④梯形ADCE的面积与△ABE的面积比是3:1,其中正确的结论的个数有( )

A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com