
【题目】在一副扑克牌中取牌面花色分别为黑桃、红心、方块各一张,洗匀后正面朝下放在桌面上.
(1)从这三张牌中随机抽取一张牌,抽到牌面花色为红心的概率是多少?
(2)小王和小李玩摸牌游戏,游戏规则如下:先由小王随机抽出一张牌,记下牌面花色后放回,洗匀后正面朝下,再由小李随机抽出一张牌,记下牌面花色.当两张牌的花色相同时,小王赢;当两张牌面的花色不相同时,小李赢.请你利用树状图或列表法分析该游戏规则对双方是否公平?并说明理由.
【答案】
(1)解:P(抽到牌面花色为红心)= ![]()
(2)解:游戏规则对双方不公平.
理由如下:
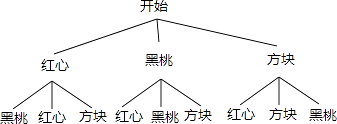
小李 小王 | 红心 | 黑桃 | 方块 |
红心 | 红心、红心 | 红心、黑桃 | 红心、方块 |
黑桃 | 黑桃、红心 | 黑桃、黑桃 | 黑桃、方块 |
方块 | 方块、红心 | 方块、黑桃 | 方块、方块 |
由树状图或表格知:所有可能出现的结果共有9种.
P(抽到牌面花色相同)= ![]() ;
;
P(抽到牌面花色不相同)= ![]() ;
;
∵ ![]() <
< ![]() ,
,
∴此游戏不公平,小李赢的可能性大.
【解析】(1)利用概率公式易得结果;(2)事件分为两个步骤,树状图可分为两层,机会均等的结果为9种,易得牌面花色相同的结果与花色不同的结果不等,概率不等,对小李有利.
【考点精析】关于本题考查的列表法与树状图法和概率公式,需要了解当一次试验要设计三个或更多的因素时,用列表法就不方便了,为了不重不漏地列出所有可能的结果,通常采用树状图法求概率;一般地,如果在一次试验中,有n种可能的结果,并且它们发生的可能性都相等,事件A包含其中的m中结果,那么事件A发生的概率为P(A)=m/n才能得出正确答案.


 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:
【题目】完成下列证明:如图,已知![]() ,
,![]() ,
,![]() .
.
求证:![]() .
.

证明:![]() ,
,![]() (已知)
(已知)
![]() ,
,![]() (_____________________)
(_____________________)
![]() (等量代换)
(等量代换)
![]() (_______________________)
(_______________________)
![]() (__________________________)
(__________________________)
又![]() (已知)
(已知)
![]() _______
_______![]() ________(等量代换)
________(等量代换)
![]() (_____________________________)
(_____________________________)
![]() (____________________).
(____________________).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校学生在电脑培训前后各参加了一次水平相同的考试,考分都以同一标准划分成“不合格”、“合格”、“优秀”三个等级.为了了解电脑培训的效果,随机抽取其中32名学生两次考试考分等级制成统计图(如图),试回答下列问题:
(1)这32名学生经过培训,考分等级“不合格”的百分比由________下降到________;
(2)估计该校640名学生,培训后考分等级为“合格”与“优秀”的学生共有多少名.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),分别以直角△ABC的三边为直径向外作三个半圆,其面积分别用S1、S2、S3表示,则不难说明S1=S2+S3。(1)如图(2),分别以直角△ABC三边为一边向外作三个正方形,其面积分别用S1、S2、S3表示,那么S1、S2、S3之间有什么关系?(2)如图(3),若分别以直角△ABC三边为一边向外作三个正三角形,其面积分别用S1、S2、S3表示,试确定S1、S2、S3之间的关系并加以说明.
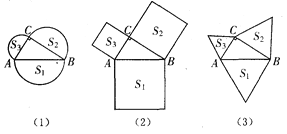
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了增强抗旱能力,保证今年夏粮丰收,某村新修建了一个蓄水池,这个蓄水池安装了两个进水管和一个出水管(两个进水管的进水速度相同)一个进水管和一个出水管的进出水速度如图(1)所示,某天0点到6点(至少打开一个水管),该蓄水池的蓄水量如图(2)所示,并给出以下三个论断:①0点到1点不进水,只出水;②1点到4点不进水,不出水;③4点到6点只进水,不出水.则一定正确的论断是( )

A.①③B.②③C.③D.①②
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)如图,已知△ABC为等边三角形,点D、E分别在BC、AC边上,且AE=CD,AD与BE相交于点F。

(1)求证:△ABE≌△CAD;(2)求∠BFD的度数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市推出如下购物优惠方案:![]() 一次性购物在80元
一次性购物在80元![]() 不含80元
不含80元![]() 以内时,不享受优惠;
以内时,不享受优惠;![]() 一次性购物在80元
一次性购物在80元![]() 含80元
含80元![]() 以上,300元
以上,300元![]() 不含300元
不含300元![]() 以内时,一律享受九折的优惠;
以内时,一律享受九折的优惠;![]() 一次性购物在300元
一次性购物在300元![]() 含300元
含300元![]() 以上时,一律享受八折的优惠,某顾客在本超市两次购物分别付款65元、252元,如果他改成在本超市一次性购买与上两次完全相同的商品,则应付款
以上时,一律享受八折的优惠,某顾客在本超市两次购物分别付款65元、252元,如果他改成在本超市一次性购买与上两次完全相同的商品,则应付款![]()
![]()
A. 316元 B. 304元或316元 C. 276元 D. 276元或304元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OABC的边OA,OC分别在x轴、y轴上,点B坐标为(4,t)(t>0),二次函数y=x2+bx(b<0)的图象经过点B,顶点为点D.
(1)当t=12时,顶点D到x轴的距离等于;
(2)点E是二次函数y=x2+bx(b<0)的图象与x轴的一个公共点(点E与点O不重合),求OEEA的最大值及取得最大值时的二次函数表达式;
(3)矩形OABC的对角线OB、AC交于点F,直线l平行于x轴,交二次函数y=x2+bx(b<0)的图象于点M、N,连接DM、DN,当△DMN≌△FOC时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,![]() ,
,![]() ,以B点为直角顶点在第二象限作等腰直角
,以B点为直角顶点在第二象限作等腰直角![]() .
.
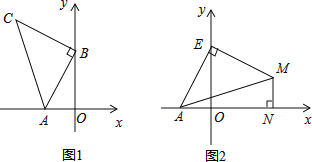
![]() 求C点的坐标;
求C点的坐标;
![]() 在坐标平面内是否存在一点P,使
在坐标平面内是否存在一点P,使![]() 与
与![]() 全等?若存在,直接写出P点坐标,若不存在,请说明理由;
全等?若存在,直接写出P点坐标,若不存在,请说明理由;
![]() 如图2,点E为y轴正半轴上一动点,以E为直角顶点作等腰直角
如图2,点E为y轴正半轴上一动点,以E为直角顶点作等腰直角![]() ,过M作
,过M作![]() 轴于N,直接写出
轴于N,直接写出![]() 的值为 .
的值为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com