
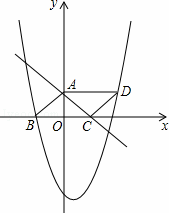
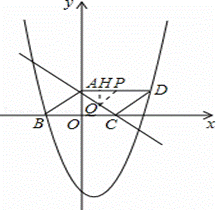
如图,三角形ABC是以BC为底边的等腰三角形,点A、C分别是一次函数y=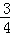 x+3的图象与y,x轴的交点,点B在二次函数
x+3的图象与y,x轴的交点,点B在二次函数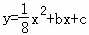 的图象上,且该二次函数图象上存在一点D使四边形ABCD能构成平行四边形。
的图象上,且该二次函数图象上存在一点D使四边形ABCD能构成平行四边形。
(1)试求b,c的值,并写出该二次函数表达式;
(2)动点P从A到D,同时动点Q从C到A都以每秒1个单位的速度运动,问:
①当P运动到何处时,有PQ⊥AC?
②当P运动到何处时,四边形PDCQ的面积最小?此时四边形PDCQ的面积是多少?
(1)由y=﹣ x+3,令x=0,得y=3,所以点A(0,3);令y=0,得x=4,所以点C(4,0),\
x+3,令x=0,得y=3,所以点A(0,3);令y=0,得x=4,所以点C(4,0),\
,∵△ABC是以BC为底边的等腰三角形,∴B点坐标为(﹣4,0),
又∵四边形ABCD是平行四边形,∴D点坐标为(8,3),将点B(﹣4,0)、点D(8,3)代入二次函数y=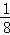 x2+bx+c,可得
x2+bx+c,可得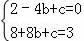 ,解得:
,解得: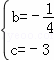 ,
,
故该二次函数解析式为:y=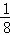 x2﹣
x2﹣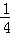 x﹣3.
x﹣3.
(2)①设点P运动了t秒时,PQ⊥AC,此时AP=t,CQ=t,AQ=5﹣t,∵PQ⊥AC,∴△APQ∽△CAO,,∴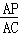 =
=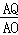 ,即
,即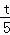 =
=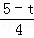 ,解得:t=
,解得:t=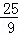 .即当点P运动到距离A点
.即当点P运动到距离A点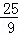 个单位长度处,有PQ⊥AC.
个单位长度处,有PQ⊥AC.
②∵S四边形PDCQ+S△APQ=S△ACD,且S△ACD=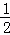 ×8×3=12,
×8×3=12,
∴当△APQ的面积最大时,四边形PDCQ的面积最小,…
当动点P运动t秒时,AP=t,CQ=t,AQ=5﹣t,
设△APQ底边AP上的高为h,作QH⊥AD于点H,由△AQH∽CAO可得: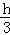 =
=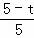 ,
,
解得:h=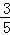 (5﹣t),,∴S△APQ=
(5﹣t),,∴S△APQ=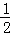 t×
t×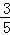 (5﹣t)=
(5﹣t)=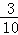 (﹣t2+5t)=﹣
(﹣t2+5t)=﹣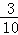 (t﹣
(t﹣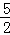 )2+
)2+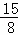 ,
,
∴当t=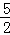 时,S△APQ达到最大值
时,S△APQ达到最大值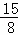 ,此时S四边形PDCQ=12﹣
,此时S四边形PDCQ=12﹣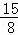 =
=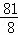
故当点P运动到距离点A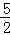 个单位处时,四边形PDCQ面积最小,最小值为
个单位处时,四边形PDCQ面积最小,最小值为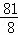 .
.


科目:初中数学 来源: 题型:
如图,△ABC中,∠BAC=90°,正方形的一边GF在BC上,其余两个顶点D,E分别在AB,AC上.连接AG,AF分别交DE于M,N两点.
(1)求证: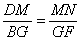 .
.
(2) 求证: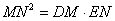 .
.
(3)若AB=AC=2,求MN的
查看答案和解析>>
科目:初中数学 来源: 题型:
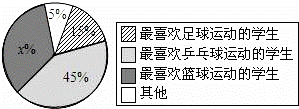
某校一课外活动小组为了解学生最喜欢的球类运动情况,随机抽查本校九年级的200名学生,调查的结果如图所示.请根据该扇形统计图解答以下问题:
(1)求图中x的值和最喜欢乒乓球运动的学生人数;
(2)若由3名最喜欢篮球运动的学生,1名最喜欢乒乓球运动的学生,1名最喜欢足球运动的学生组队外出参加一次联谊活动.欲从中选出2人担任组长(不分正副),列出所有可能情况,并求2人均是最喜欢篮球运动的学生的概率。
查看答案和解析>>
科目:初中数学 来源: 题型:
设边长为2的正方形的对角线长为a下列关于a的四种说法:①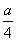 是分数;②a可以用数轴上的一个点来表示;③3<a<4;④a是8的算术平方根。其中所有正确说法的序号是( )
是分数;②a可以用数轴上的一个点来表示;③3<a<4;④a是8的算术平方根。其中所有正确说法的序号是( )
A.①④ B.②④ C.①②④ D.①③
查看答案和解析>>
科目:初中数学 来源: 题型:
甲、乙两盒中各放入分别写有数字1,2,3的三张卡片,每张卡片除数字
外其他完全相同.从甲盒中随机抽出一张卡片,再从乙盒中随机摸出一张
卡片,摸出的两张卡片上的数字之和是3的概率是( )
A.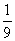 B.
B.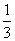 C.
C.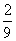 D.
D.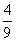
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com