
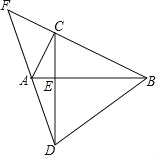
【题目】如图,Rt△ABC中,∠ACB=90°,CD⊥AB于E,CD=AB,DA、BC延长线交于F.
(1)若AC=12,∠ABC=30°,求DE的长;
(2)若BC=2AC,求证:DA=![]() FC.
FC.
【答案】(1)![]() ;(2)见解析.
;(2)见解析.
【解析】
(1)在Rt△ABC中,∠ACB=90°,AC=12,∠ABC=30°,可求得AB,BC的长,再在Rt△CEB中,求得CE的长,进而得出DE的长;
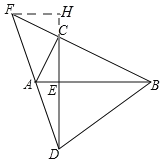
(2)作FH垂直CD交DC的延长线于点H,利用tan∠CFH=tan∠ACE=tan∠CBA![]() ,可设AE=a,CE=2a,CH=m,FH=2m,根据△DEA∽△DHF得出m=a,再利用勾股定理可得出DA
,可设AE=a,CE=2a,CH=m,FH=2m,根据△DEA∽△DHF得出m=a,再利用勾股定理可得出DA![]() FC.
FC.
Rt△ABC中,∠ACB=90°,AC=12,∠ABC=30°,
∴CD=AB=24,BC=12![]() .
.
∵CD⊥AB于E,
∴CE![]() BC=6
BC=6![]() ,
,
∴DE=CD﹣CE=24﹣6![]() .
.
(2)如图,作FH垂直CD交DC的延长线于点H.
∵∠ACB=90°,BC=2AC,
∴tan∠CBA![]() .
.
∵CD⊥AB于E,
∴∠CFH=∠ACE=∠CBA,
∴设AE=a,CE=2a,CH=m,FH=2m,
∴BE=4a,AB=a+4a=5a,
∴DC=AB=5a,
∴DE=3a.
∵AE∥FH,
∴△DEA∽△DHF,
∴![]() ,∴m=a.
,∴m=a.
∵DA![]() ,FC
,FC![]() ,
,
∴DA![]() FC.
FC.


科目:初中数学 来源: 题型:
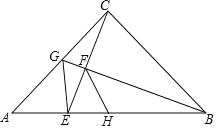
【题目】如图,△ABC中,∠ACB=90°,AC=BC,点G为AC中点,连结BG,CE⊥BG于F,交AB于E,连接GE,点H为AB中点,连接FH.以下结论:(1)∠ACE=∠ABG;(2)∠AGE=∠CGB:(3)若AB=10![]() ,则BF=4
,则BF=4![]() ;(4)FH平分∠BFE;(5)S△BGC=3S△CGE.其中正确结论的个数是( )
;(4)FH平分∠BFE;(5)S△BGC=3S△CGE.其中正确结论的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形ABCD的面积为300cm2,长和宽的比为3:2.在此长方形内沿着边的方向能否并排裁出两个面积均为147cm2的圆(π取3),请通过计算说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
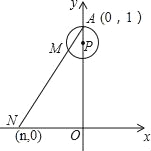
【题目】如图,在直角坐标系xOy中,已知点A(0,1),点P在线段OA上,以AP为半径的⊙P周长为1.点M从A开始沿⊙P按逆时针方向转动,射线AM交x轴于点N(n,0),设点M转过的路程为m(0<m<1).
(1)当m=![]() 时,n=_____;
时,n=_____;
(2)随着点M的转动,当m从![]() 变化到
变化到![]() 时,点N相应移动的路径长为_____.
时,点N相应移动的路径长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市举行“行动起来,对抗雾霾”为主题的植树活动,某街道积极响应,决定对该街道进行绿化改造,共购进甲、乙两种树共50棵,已知甲树每棵800元,乙树每棵1200元.
(1)若购买两种树的总金额为56000元,求甲、乙两种树各购买了多少棵?
(2)若购买甲树的金额不少于购买乙树的金额,至少应购买甲树多少棵?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校七年级春游,现有36座和42座两种客车供选择租用,若只租用36座客车若干辆,则正好坐满;若只租用42座客车,则能少租一辆,且有一辆车没有坐满,但超过30人;已知36座客车每辆租金400元,42座客车每辆租金440元.
(1)该校七年级共有多少人参加春游?
(2)请你帮该校设计一种最省钱的租车方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
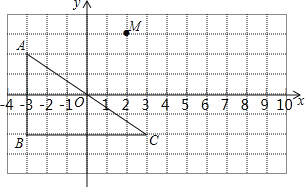
【题目】如图,已知Rt△ABC的三个顶点分别为A(-3,2),B(-3,-2),C(3,-2).将△ABC平移,使点A与点M(2,3)重合,得到△MNP.
(1)将△ABC向 平移 个单位长度,然后再向 平移 个单位长度,可以得到△MNP.
(2)画出△MNP.
(3)在(1)的平移过程中,线段AC扫过的面积为 (只需填入数值,不必写单位).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com