
【题目】某市举行“行动起来,对抗雾霾”为主题的植树活动,某街道积极响应,决定对该街道进行绿化改造,共购进甲、乙两种树共50棵,已知甲树每棵800元,乙树每棵1200元.
(1)若购买两种树的总金额为56000元,求甲、乙两种树各购买了多少棵?
(2)若购买甲树的金额不少于购买乙树的金额,至少应购买甲树多少棵?
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】以下说法合理的是:( )
A. “打开电视,正在播放新闻节日”是必然事件
B. “抛一枚硬币,正面朝上的概率为![]() ”表示每抛两次就有一次正面朝上
”表示每抛两次就有一次正面朝上
C. “抛掷一枚均匀的骰子,出现点数6的概率是![]() ”表示随着抛掷次数的增加“出现点数6”这一事件发生的频率稳定在
”表示随着抛掷次数的增加“出现点数6”这一事件发生的频率稳定在![]() 附近
附近
D. 为了解某品牌火腿的质量,选择全面检测
查看答案和解析>>
科目:初中数学 来源: 题型:
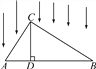
【题目】如图所示,△ABC被平行光线照射,CD⊥AB于D,AB在投影面上.
(1)指出图中AC的投影是什么?CD与BC的投影呢?
(2)探究:当△ABC为直角三角形(∠ACB=90°)时,易得AC2=AD·AB,此时有如下结论:直角三角形一直角边的平方等于它在斜边射影与斜边的乘积,这一结论我们称为射影定理.通过上述结论的推理,请证明以下两个结论.
①BC2=BD·AB;②CD2=AD·BD.
查看答案和解析>>
科目:初中数学 来源: 题型:
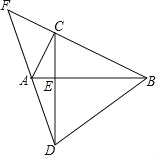
【题目】如图,Rt△ABC中,∠ACB=90°,CD⊥AB于E,CD=AB,DA、BC延长线交于F.
(1)若AC=12,∠ABC=30°,求DE的长;
(2)若BC=2AC,求证:DA=![]() FC.
FC.
查看答案和解析>>
科目:初中数学 来源: 题型:
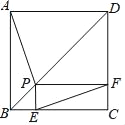
【题目】如图,P为边长为2的正方形ABCD的对角线BD上任一点,过点P作PE⊥BC于点E,PF⊥CD于点F,连接EF.给出以下4个结论:①AP=EF;②AP⊥EF;③EF最短长度为![]() ;④若∠BAP=30°时,则EF的长度为2.其中结论正确的有( )
;④若∠BAP=30°时,则EF的长度为2.其中结论正确的有( )
A. ①②③B. ①②④C. ②③④D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
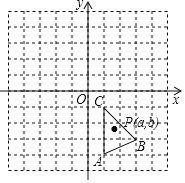
【题目】如图所示,三角形![]() (记作
(记作![]() )在方格中,方格纸中的每个小方格都是边长为1个单位的正方形,三个顶点的坐标分别是
)在方格中,方格纸中的每个小方格都是边长为1个单位的正方形,三个顶点的坐标分别是![]() ,
,![]() ,
,![]() ,先将
,先将![]() 向上平移3个单位长度,再向右平移2个单位长度,得到
向上平移3个单位长度,再向右平移2个单位长度,得到![]() .
.

(1)在图中画出![]() ;
;
(2)点![]() ,
,![]() 的坐标分别为______、______;
的坐标分别为______、______;
(3)若![]() 轴有一点
轴有一点![]() ,使
,使![]() 与
与![]() 面积相等,求出
面积相等,求出![]() 点的坐标.
点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电子厂生产一种新型电子产品,每件制造成本为20元,试销过程中发现,每月销售量y(万件)与销售单价x(元)之间的关系可以近似地看作一次函数y=﹣2x+100.(利润=售价﹣制造成本)
(1)写出每月的利润z(万元)与销售单价x(元)之间的函数关系式;
(2)当销售单价为多少元时,厂商每月获得的利润为400万元?
(3)根据相关部门规定,这种电子产品的销售单价不能高于40元,如果厂商每月的制造成本不超过520万元,那么当销售单价为多少元时,厂商每月获得的利润最大?最大利润为多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,-4),B(3,-3),C(1,-1).
(1)将△ABC先向上平移5个单位,再向左平移3个单位,画出平移后得到的△A1B1C1;
(2)写出△A1B1C1各顶点的坐标;
(3)若△ABC内有一点P(a,b),请写出平移后得到的对应点P1的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
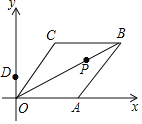
【题目】已知菱形OABC在平面直角坐标系的位置如图所示,顶点A(5,0),OB=4![]() ,点P是对角线OB上的一个动点,D(0,1),当CP+DP最短时,点P的坐标为( )
,点P是对角线OB上的一个动点,D(0,1),当CP+DP最短时,点P的坐标为( )
A. (0,0)B. (1,![]() )C. (
)C. (![]() ,
,![]() )D. (
)D. (![]() ,
,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com