
【题目】如图,P为边长为2的正方形ABCD的对角线BD上任一点,过点P作PE⊥BC于点E,PF⊥CD于点F,连接EF.给出以下4个结论:①AP=EF;②AP⊥EF;③EF最短长度为![]() ;④若∠BAP=30°时,则EF的长度为2.其中结论正确的有( )
;④若∠BAP=30°时,则EF的长度为2.其中结论正确的有( )
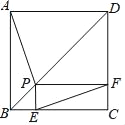
A. ①②③B. ①②④C. ②③④D. ①③④
【答案】A
【解析】
连接PC,可证得△ABP≌△CBP,结合矩形的性质,可证得PA=EF,国判断①;延长AP交BC于点G,可证得AP⊥EF,可判断②;求得AP的最小值即可求得EF的最短长度,可判断③;当点P在点B或点D时,AP有最大值2,则可判断④;可求得答案.
解:
①如图,连接PC,
∵四边形ABCD为正方形,
∴AB=BC,∠ABP=∠CBP=45°,
在△ABP和△CBP中
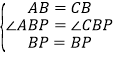
∴△ABP≌△CBP(SAS),
∴AP=PC,
∵PE⊥BC,PF⊥CD,且∠FCE=90°,
∴四边形PECF为矩形,
∴PC=EF,
∴AP=EF,故①正确;
②延长AP交BC于点G,
由①可得∠PCE=∠PFE=∠BAP,
∵PE∥AB,
∴∠EPG=∠BAP,
∴∠EPG=∠PFE,
∵∠EPF=90°,
∴∠EPG+∠PEF=∠PEG+∠PFE=90°,
∴AP⊥EF,故②正确;
③当AP⊥BD时,AP有最小值![]() ,此时P为BD的中点,
,此时P为BD的中点,
由①可知EF=AP,
∴EF的最短长度为![]() ,故③正确;
,故③正确;
④当点P在点B或点D位置时,AP=AB=2,
∴EF=AP≤2,
∴当∠BAP=30°时,AP<2,
即EF的长度不可能为2,故④不正确;
综上可知正确的结论为①②③,
故选:A.


科目:初中数学 来源: 题型:
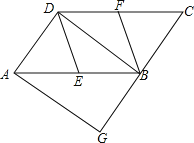
【题目】如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,过A点作AG∥DB,交CB的延长线于点G.
(1)求证:DE∥BF;
(2)若∠G=90,求证:四边形DEBF是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,BC=8cm,射线AG∥BC,点E从点A出发沿射线AG以1cm/s的速度运动,同时点F从点B出发沿射线BC以2cm/s的速度运动,设运动时间为t(s).
(1)连接EF,当EF经过AC边的中点D时,求证:△ADE≌△CDF;
(2)①当t为 时,以A、F、C、E为顶点的四边形是平行四边形(直接写出结果);
②当t为 时,四边形ACFE是菱形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长方形ABCD的面积为300cm2,长和宽的比为3:2.在此长方形内沿着边的方向能否并排裁出两个面积均为147cm2的圆(π取3),请通过计算说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个四位正整数m各个数位上的数字互不相同且都不为0,四位数m的前两位数字之和为5,后两位数字之和为11,称这样的四位数m为“半期数”;把四位数m的各位上的数字依次轮换后得到新的四位数m′,设m′=![]() ,在m′的所有可能的情况中,当|b+2c﹣a﹣d|最小时,称此时的m′是m的“伴随数”,并规定F(m′)=a2+c2﹣2bd;例如:m=2365,则m′为:3652,6523,5236,因为|6+10﹣3﹣2|=11,|5+4﹣6﹣3|=0,|2+6﹣5﹣6|=3,0最小,所以6523叫做2365的“伴随数”,F(5236)=52+32﹣2×2×6=10.
,在m′的所有可能的情况中,当|b+2c﹣a﹣d|最小时,称此时的m′是m的“伴随数”,并规定F(m′)=a2+c2﹣2bd;例如:m=2365,则m′为:3652,6523,5236,因为|6+10﹣3﹣2|=11,|5+4﹣6﹣3|=0,|2+6﹣5﹣6|=3,0最小,所以6523叫做2365的“伴随数”,F(5236)=52+32﹣2×2×6=10.
(1)最大的四位“半期数”为 ;“半期数”3247的“伴随数”是 .
(2)已知四位数P=![]() 是“半期数”,三位数Q=
是“半期数”,三位数Q=![]() ,且441Q﹣4P=88991,求F(P')的最大值.
,且441Q﹣4P=88991,求F(P')的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市举行“行动起来,对抗雾霾”为主题的植树活动,某街道积极响应,决定对该街道进行绿化改造,共购进甲、乙两种树共50棵,已知甲树每棵800元,乙树每棵1200元.
(1)若购买两种树的总金额为56000元,求甲、乙两种树各购买了多少棵?
(2)若购买甲树的金额不少于购买乙树的金额,至少应购买甲树多少棵?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边 ABC 的边长是 2 , D 、 E 分别为 AB 、 AC 的中点,连接CD ,过 E 点作 EF // DC 交 BC 的延长线于点 F
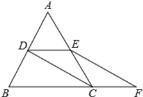
(1) 求证:四边形 CDEF 是平行四边形;
(2)求四边形 CDEF 的周长
查看答案和解析>>
科目:初中数学 来源: 题型:
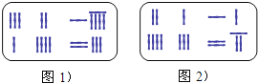
【题目】《九章算术》是我国东汉初年编订的一部数学经典著作.在它的“方程”一章里,一次方程组是由算筹布置而成的.《九章算术》中的算筹图是竖排的,为看图方便,我们把它改为横排,如图1、图2.图中各行从左到右列出的算筹数分别表示未知数x,y的系数与相应的常数项.把图1所示的算筹图用我们现在所熟悉的方程组形式表述出来,就是![]() ,类似地,图2所示的算筹图我们可以表述为( )
,类似地,图2所示的算筹图我们可以表述为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直角梯形ABCD中,AD∥BC,∠ADC=90°,AD=8,BC=6,点M从点D出发,以每秒2个单位长度的速度向点A运动,同时,点N从点B出发,以每秒1个单位长度的速度向点C运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点N作NP⊥AD于点P,连接AC交NP于点Q,连接MQ.设运动时间为t秒.

(1)AM= ,AP= .(用含t的代数式表示)
(2)当四边形ANCP为平行四边形时,求t的值
(3)如图2,将△AQM沿AD翻折,得△AKM,是否存在某时刻t,
①使四边形AQMK为为菱形,若存在,求出t的值;若不存在,请说明理由
②使四边形AQMK为正方形,则AC= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com