
【题目】一个四位正整数m各个数位上的数字互不相同且都不为0,四位数m的前两位数字之和为5,后两位数字之和为11,称这样的四位数m为“半期数”;把四位数m的各位上的数字依次轮换后得到新的四位数m′,设m′=![]() ,在m′的所有可能的情况中,当|b+2c﹣a﹣d|最小时,称此时的m′是m的“伴随数”,并规定F(m′)=a2+c2﹣2bd;例如:m=2365,则m′为:3652,6523,5236,因为|6+10﹣3﹣2|=11,|5+4﹣6﹣3|=0,|2+6﹣5﹣6|=3,0最小,所以6523叫做2365的“伴随数”,F(5236)=52+32﹣2×2×6=10.
,在m′的所有可能的情况中,当|b+2c﹣a﹣d|最小时,称此时的m′是m的“伴随数”,并规定F(m′)=a2+c2﹣2bd;例如:m=2365,则m′为:3652,6523,5236,因为|6+10﹣3﹣2|=11,|5+4﹣6﹣3|=0,|2+6﹣5﹣6|=3,0最小,所以6523叫做2365的“伴随数”,F(5236)=52+32﹣2×2×6=10.
(1)最大的四位“半期数”为 ;“半期数”3247的“伴随数”是 .
(2)已知四位数P=![]() 是“半期数”,三位数Q=
是“半期数”,三位数Q=![]() ,且441Q﹣4P=88991,求F(P')的最大值.
,且441Q﹣4P=88991,求F(P')的最大值.
【答案】(1)4192,7324;(2)42.
【解析】
(1)根据“半期数”的定义分析最大的四位“半期数”应该是千位最大,最大只能为4,所以百位是1,十位最大是9,个位是2,所以最大半期数为:4192,分析3247的所有可能为,2473,4732,7324.根据题意|b+2c﹣a﹣d|最小的数是7324,所以3247的“伴随数”是:7324.
(2)根据定义可知a+b=5,c+d=11.再根据441Q﹣4P=88991,可以算出P的值,从而求出F(P')的最大值.
解;(1)根据题意可得最大的四位“半期数”应该是千位最大,最大只能为4,所以百位是1,十位最大是9,个位是2,所以最大半期数为:4192.
∵3247的所有可能为,2473,4732,7324.
∵|4+14﹣2﹣3|=13,|7+6﹣4﹣2|=7,|3+4﹣7﹣4|=4, 4最小,所以7324为3247的“伴随数”.
故答案为:4192;7324.
(2)∵P为“半期数”
∴a+b=5,c+d=11,∴b=5﹣a,d=11﹣c,∴P=1000a+100(5﹣a)+10c+11﹣c=900a+9c+511.
∵Q=200+10a+c,∴441Q﹣4P=88991,∴441(200+10a+c)﹣4(900a+9c+511)=88991
化简得:2a+c=7
①当a=1时,c=5,此时这个四位数为1456符合题意;
②当a=2时,c=3,此时这个四位数为2338不符合题意,舍去;
③当a=3时,c=1,不符合题意,舍去;
综上所述:这个四位数只能是1456,则P'可能为4561,5614,6145.
∵|5+12﹣4﹣1|=12,|6+2﹣5﹣4|=1,|1+8﹣6﹣5|=2,1最小,所以5614为P的“伴随数”,∴F(5614)=a2+c2﹣2bd=25+1﹣2×6×4=﹣22;
F(4561)=a2+c2﹣2bd=16+36﹣2×5×1=42;
F(6145)=a2+c2﹣2bd=36+16﹣2×1×5=42;
∴F(P')的最大值为42.


科目:初中数学 来源: 题型:
【题目】如图,∠MON=90°,矩形ABCD的顶点A、B分别在边OM,ON上,当B在边ON上运动时,A随之在OM上运动,矩形ABCD的形状保持不变,其中AB=2,BC=1,运动过程中,点D到点O的最大距离为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】填空,把下面的推理过程补充完整,并在括号内注明理由:
如图,已知A、B、C、D在同一直线上,AE∥DF,AC=BD,∠E=∠F,求证:BE∥CF.

证明:∵AE∥DF(已知)
∴_________(两直线平行,内错角相等)
∵AC=BD(已知)
又∵AC=AB+BC,BD=BC+CD
∴________(等式的性质)
∵∠E=∠F(已知)
∴△ABE≌△DCF(___________)
∴∠ABE=∠DCF(_________________)
∵ABF+∠CBE=180°,∠DCF+∠BCF=180°
∴∠CBE=∠BCF(__________________)
∴BE∥CF(________________________)
查看答案和解析>>
科目:初中数学 来源: 题型:
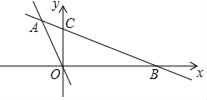
【题目】如图,在平面直角坐标系中,直线AB分别与x轴、y轴交于点B、C,与直线OA交于点A.已知点A的坐标为(﹣3,5),OC=4.
(1)分别求出直线AB、AO的解析式;
(2)求△ABO的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年“五一节”前,某商场用60万元购进某种商品,该商品有甲、乙两种包装共500件,其中每件甲包装中有75个A种产品,每个A产品的成本为12元;每件乙包装中有100个B产品,每个B种产品的成本为14元.商场将A产品标价定为每个18元,B产品标价定为每个20元.
(1)甲、乙两种包装的产品各有多少件?
(2)“五一节”商场促销,将A产品按原定标价打9折销售,B种产品按原定标价打8.5折销售,“五一节”期间该产品全部卖完,该商场销售该商品共获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P为边长为2的正方形ABCD的对角线BD上任一点,过点P作PE⊥BC于点E,PF⊥CD于点F,连接EF.给出以下4个结论:①AP=EF;②AP⊥EF;③EF最短长度为![]() ;④若∠BAP=30°时,则EF的长度为2.其中结论正确的有( )
;④若∠BAP=30°时,则EF的长度为2.其中结论正确的有( )
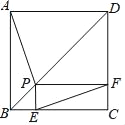
A. ①②③B. ①②④C. ②③④D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
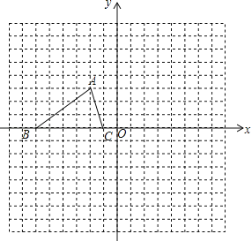
【题目】如图,已知△ABC的三个顶点坐标为A(﹣2,3),B(﹣6,0),C(﹣1,0).
(1)将△ABC绕坐标原点O旋转180°,画出图形,并写出点A的对应点A′的坐标_____;
(2)将△ABC绕坐标原点O逆时针旋转90°,直接写出点A的对应点A″的坐标_____;
(3)请直接写出:以A、B、C为顶点的平行四边形的第四个顶点D的所有可能的坐标_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O是正△ABC内一点,OA=3,OB=4,OC=5,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,下列结论:①△BO′A可以由△BOC绕点B逆时针旋转60°得到;②点O与O′的距离为4;③∠AOB=150°;④S四边形AOBO′=6+4![]() ;⑤S△AOC+S△AOB=6+
;⑤S△AOC+S△AOB=6+![]() ,其中正确的结论是( )
,其中正确的结论是( )

A. ①②③⑤ B. ①②③④ C. ①②④⑤ D. ①②③④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一种实验用轨道弹珠,在轨道上行驶5分钟后离开轨道,前2分钟其速度v(米/分)与时间t(分)满足二次函数v=at2,后三分钟其速度v(米/分)与时间t(分)满足反比例函数关系,如图,轨道旁边的测速仪测得弹珠1分钟末的速度为2米/分,求:

(1)二次函数和反比例函数的关系式.
(2)弹珠在轨道上行驶的最大速度.
(3)求弹珠离开轨道时的速度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com