
【题目】如图,∠MON=90°,矩形ABCD的顶点A、B分别在边OM,ON上,当B在边ON上运动时,A随之在OM上运动,矩形ABCD的形状保持不变,其中AB=2,BC=1,运动过程中,点D到点O的最大距离为_____.

科目:初中数学 来源: 题型:
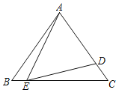
【题目】如图,在△ABC中,AB=AC=6,点D在边AC上,AD的中垂线交BC于点E.若∠AED=∠B,CE=3BE,则CD等于( )
A. ![]() B. 2C.
B. 2C. ![]() D. 3
D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知A(0,a),B(b,0),C(b,c)三点,其中a,b,c满足关系式![]() .
.
(1)求a,b,c的值;
(2)如果在第二象限内有一点P(m,![]() ),使四边形ABOP的面积与三角形ABC的面积相等?若存在,求出点P的坐标;若不存在,请说明理由.
),使四边形ABOP的面积与三角形ABC的面积相等?若存在,求出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 中,点
中,点![]() 是
是![]() 延长线上的一点,过点
延长线上的一点,过点![]() 作
作![]() ,
,![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,
,![]() 与
与![]() 交于点
交于点![]() .
.

(1)如图1,若![]() ,
,![]() ,直接求出
,直接求出![]() 的度数:__________;
的度数:__________;
(2)如图2,若![]() ,试判断
,试判断![]() 与
与![]() 的数量关系,并证明你的结论;
的数量关系,并证明你的结论;
(3)如图3,若![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在横线上完成下面的证明,并在括号内注明理由.
已知:如图,∠ABC+∠BGD=180°,∠1=∠2.
求证:EF∥DB.
证明:∵∠ABC+∠BGD=180°,(已知)
∴ .( )
∴∠1=∠3.( )
又∵∠1=∠2,(已知)
∴ .( )
∴EF∥DB.( )

查看答案和解析>>
科目:初中数学 来源: 题型:
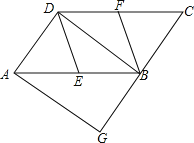
【题目】如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,过A点作AG∥DB,交CB的延长线于点G.
(1)求证:DE∥BF;
(2)若∠G=90,求证:四边形DEBF是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD,BC于点E,F,垂足为点O.
(1)连接AF,CE,求证:四边形AFCE为菱形;
(2)求菱形AFCE的边长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个四位正整数m各个数位上的数字互不相同且都不为0,四位数m的前两位数字之和为5,后两位数字之和为11,称这样的四位数m为“半期数”;把四位数m的各位上的数字依次轮换后得到新的四位数m′,设m′=![]() ,在m′的所有可能的情况中,当|b+2c﹣a﹣d|最小时,称此时的m′是m的“伴随数”,并规定F(m′)=a2+c2﹣2bd;例如:m=2365,则m′为:3652,6523,5236,因为|6+10﹣3﹣2|=11,|5+4﹣6﹣3|=0,|2+6﹣5﹣6|=3,0最小,所以6523叫做2365的“伴随数”,F(5236)=52+32﹣2×2×6=10.
,在m′的所有可能的情况中,当|b+2c﹣a﹣d|最小时,称此时的m′是m的“伴随数”,并规定F(m′)=a2+c2﹣2bd;例如:m=2365,则m′为:3652,6523,5236,因为|6+10﹣3﹣2|=11,|5+4﹣6﹣3|=0,|2+6﹣5﹣6|=3,0最小,所以6523叫做2365的“伴随数”,F(5236)=52+32﹣2×2×6=10.
(1)最大的四位“半期数”为 ;“半期数”3247的“伴随数”是 .
(2)已知四位数P=![]() 是“半期数”,三位数Q=
是“半期数”,三位数Q=![]() ,且441Q﹣4P=88991,求F(P')的最大值.
,且441Q﹣4P=88991,求F(P')的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com