
【题目】已知![]() 中,点
中,点![]() 是
是![]() 延长线上的一点,过点
延长线上的一点,过点![]() 作
作![]() ,
,![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,
,![]() 与
与![]() 交于点
交于点![]() .
.

(1)如图1,若![]() ,
,![]() ,直接求出
,直接求出![]() 的度数:__________;
的度数:__________;
(2)如图2,若![]() ,试判断
,试判断![]() 与
与![]() 的数量关系,并证明你的结论;
的数量关系,并证明你的结论;
(3)如图3,若![]() ,求证:
,求证:![]() .
.
【答案】(1)25°;(2)![]() ,证明略;(3)证明略;
,证明略;(3)证明略;
【解析】
(1)先根据三角形的内角和得∠ABC=40°,分别根据角平分线的定义和三角形外角的性质得∠G的度数;
(2)根据三角形外角的性质分别表示∠BCD和∠DFC的度数,可得∠A和∠G的关系;
(3)根据平行线的性质和角平分线定义可得结论.
如图1,

∵∠ACB=90°,∠A=50°,
∴∠ABC=40°,
∵BG平分∠ABC,
∴∠CBG=20°,
∵DE∥BC,
∴∠CDE=∠BCD=90°,
∵DG平分∠ADE,
∴∠CDF=45°,
∴∠CFD=45°,
∵∠CFD=∠FBG+∠G,
∴∠G=45°-20°=25°;
(2)如图2,∠A=2∠G,

理由是:由(1)知:∠ABC=2∠FBG,∠CDF=∠CFD,
∵BC∥DE,
∴∠BCD=∠CDE,
∵∠BCD=∠A+∠ABC=∠A+2∠FBG,
∴2∠FBG+∠A=2∠CDF,
∴∠A=2(∠CDF-∠FBG),
∵∠CFD=∠FBG+∠G,
∴∠G=∠CFD-∠FBG=∠CDF-∠FBG,
∴∠A=2∠G;
(3)如图3,

∵EF∥AD,
∴∠DFE=∠CDF,
由(2)得:∠CFD=∠CDF,
∴∠DFE=∠CFD=∠FBG+∠G=![]() ∠ABC+∠G.
∠ABC+∠G.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源: 题型:
【题目】已知方程组![]() 的解x、y满足:x为非正数,y为负数.
的解x、y满足:x为非正数,y为负数.
(1)求a的取值范围;
(2)在a的取值范围中,当a为何整数时,关于x的不等式2ax+x>2a+1的解集为x<1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在⊙O中,直径AB=6,BC是弦,∠ABC=30°,点P在BC上,点Q在⊙O上,且OP⊥PQ.
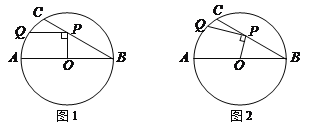
(1)如图1,当PQ∥AB时,求PQ的长度;
(2)如图2,当点P在BC上移动时,求PQ长的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,第一象限内长方形ABCD,AB∥y轴,点A(1,1),点C(a,b),满足![]() +|b﹣3|=0.
+|b﹣3|=0.
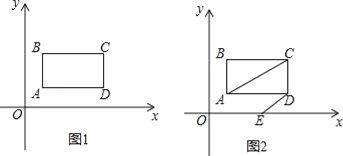
(1)求长方形ABCD的面积.
(2)如图2,长方形ABCD以每秒1个单位长度的速度向右平移,同时点E从原点O出发沿x轴以每秒2个单位长度的速度向右运动,设运动时间为t秒.
①当t=4时,直接写出三角形OAC的面积为 ;
②若AC∥ED,求t的值;
(3)在平面直角坐标系中,对于点P(x,y),我们把点P′(﹣y+1,x+1)叫做点P的伴随点,已知点A1的伴随点为A2,点A2的伴随点为A3,点A3的伴随点为A4,…,这样依次得到点A1,A2,A3,…,An.
①若点A1的坐标为(3,1),则点A3的坐标为 ,点A2014的坐标为 ;
②若点A1的坐标为(a,b),对于任意的正整数n,点An均在x轴上方,则a,b应满足的条件为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
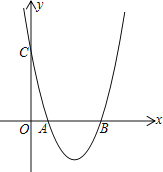
【题目】如图1,抛物线y=x2+bx+c与x轴交于A(1,0)、B(4,0),与y轴交于点C
(1) 求抛物线的解析式
(2) 抛物线上一点D,满足S△DAC=S△OAC,求点D的坐标
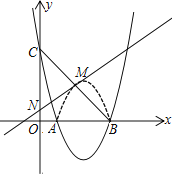
(3) 如图2,已知N(0,1),将抛物线在点A、B之间部分(含点A、B)沿x轴向上翻折,得到图T(虚线部分),点M为图象T的顶点.现将图象保持其顶点在直线MN上平移,得到的图象T1与线段BC至少有一个交点,求图象T1的顶点横坐标的取值范围
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠MON=90°,矩形ABCD的顶点A、B分别在边OM,ON上,当B在边ON上运动时,A随之在OM上运动,矩形ABCD的形状保持不变,其中AB=2,BC=1,运动过程中,点D到点O的最大距离为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等腰△ABC中,AB=AC,∠A=36°,D是AC上的一点,AD=BD,则以下结论中正确的有( )
①△BCD是等腰三角形;②点D是线段AC的黄金分割点;③△BCD∽△ABC;④BD平分∠ABC.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
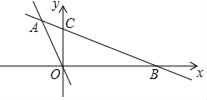
【题目】如图,在平面直角坐标系中,直线AB分别与x轴、y轴交于点B、C,与直线OA交于点A.已知点A的坐标为(﹣3,5),OC=4.
(1)分别求出直线AB、AO的解析式;
(2)求△ABO的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com