
【题目】如图1,直角梯形ABCD中,AD∥BC,∠ADC=90°,AD=8,BC=6,点M从点D出发,以每秒2个单位长度的速度向点A运动,同时,点N从点B出发,以每秒1个单位长度的速度向点C运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点N作NP⊥AD于点P,连接AC交NP于点Q,连接MQ.设运动时间为t秒.

(1)AM= ,AP= .(用含t的代数式表示)
(2)当四边形ANCP为平行四边形时,求t的值
(3)如图2,将△AQM沿AD翻折,得△AKM,是否存在某时刻t,
①使四边形AQMK为为菱形,若存在,求出t的值;若不存在,请说明理由
②使四边形AQMK为正方形,则AC= .
【答案】(1)8﹣2t;2+t;(2)2;(3)①存在时刻t=1,使四边形AQMK为菱形.理由详见解析;②8![]() .
.
【解析】试题分析:(1)由DM=2t,根据AM=AD-DM即可求出AM=6-2t;先证明四边形CNPD为矩形,得出DP=CN=4-t,则AP=AD-DP=2+t;
(2)根据四边形ANCP为平行四边形时,可得4-t=6-(6=4-t),解方程即可;
(3))①由NP⊥AD,QP=PK,可得当PM=PA时有四边形AQMK为菱形,列出方程4-t-2t=6-(4-t),求解即可,
②要使四边形AQMK为正方形,由∠ADC=90°,可得∠CAD=45°,所以四边形AQMK为正方形,则CD=AD,由AD=8,可得CD=6,利用勾股定理求得AC即可.
试题解析:(1)6﹣2t,2+t.
(2)∵四边形ANCP为平行四边形时,CN=AP,
∴4﹣t=t+2,解得t=1,
(3)①∵NP⊥AD,QP=PK,
∴当PM=PA时有四边形AQMK为菱形,
∴4﹣t﹣2t=2+t,解得t=0.5,
∴存在时刻t=0.5,使四边形AQMK为菱形.
②AC=6![]() .
.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:
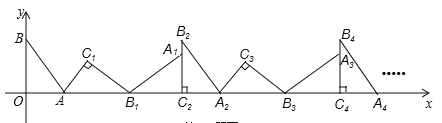
【题目】如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去….若点A(![]() ,0),B(0,2),则点B2016的坐标为______________.
,0),B(0,2),则点B2016的坐标为______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某学校开展“远是君山,磨砺意志,保护江豚,爱鸟护鸟”为主题的远足活动.已知学校与君山岛相距24千米,远足服务人员骑自行车,学生步行,服务人员骑自行车的平均速度是学生步行平均速度的2.5倍,服务人员与学生同时从学校出发,到达君山岛时,服务人员所花时间比学生少用了3.6小时,求学生步行的平均速度是多少千米/小时.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,﹣1).
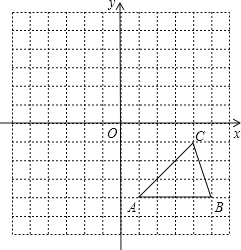
(1)试作出△ABC以C为旋转中心,沿顺时针方向旋转90°后的图形△A1B1C;
(2)以原点O为对称中心,再画出与△ABC关于原点O对称的△A2B2C2,并写出点C2的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com