
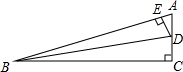
 如图,在Rt△ABC中,∠C=90°,点D,E分别在边AC,AB上,BD是∠ABC的平分线,DE⊥AB,AE=10,cosA=$\frac{5}{13}$.
如图,在Rt△ABC中,∠C=90°,点D,E分别在边AC,AB上,BD是∠ABC的平分线,DE⊥AB,AE=10,cosA=$\frac{5}{13}$.分析 (1)根据题目中的数据和锐角三角函数可以求得AD、CD的长;
(2)根据题意和角平分线的性质、勾股定理和锐角三角函数可以解答本题.
解答 解:(1)∵DE⊥AB,AE=10,cosA=$\frac{5}{13}$,
∴cosA=$\frac{AE}{AD}=\frac{5}{13}$,
解得,AD=26,
∴DE=$\sqrt{A{D}^{2}-A{E}^{2}}$=24,
∵BD是∠ABC的平分线,DE⊥AB,∠C=90°,
∴DE=CD,
∴CD=24,
即AD=26,CD=24;
(2)∵AD=26,CD=24,cosA=$\frac{5}{13}$,
∴AC=AD+CD=50,
∴AB=130,
∵AE=10,
∴BE=140,
∵BD是∠ABC的平分线,DE⊥AB,∠C=90°,
∴DE=CD,BD=BD,
∴Rt△BED≌Rt△BCD(HL),
∴BC=BE=140,
∵CD=24,
∴tan∠DBC=$\frac{CD}{BC}=\frac{24}{140}=\frac{6}{35}$.
点评 本题考查解直角三角形,解题的关键是明确题意,找出所求问需要的条件.


科目:初中数学 来源: 题型:解答题
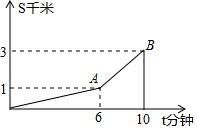 小强骑车从家到学校要经过一段先上坡后下坡的路,在这段路上小强骑车的距离s(千米)与骑车的时间t(分钟)之间的函数关系如图所示,请根据图中信息回答下列问题:
小强骑车从家到学校要经过一段先上坡后下坡的路,在这段路上小强骑车的距离s(千米)与骑车的时间t(分钟)之间的函数关系如图所示,请根据图中信息回答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
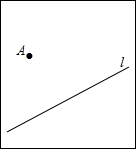 点A表示某村的一个蓄水池,l表示一条小河,为了将河水引入蓄水池,现在决定修建一条引水管道,请你在图中画出修建的这条管道的最短路线.并说明理由:
点A表示某村的一个蓄水池,l表示一条小河,为了将河水引入蓄水池,现在决定修建一条引水管道,请你在图中画出修建的这条管道的最短路线.并说明理由:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,AB=AC,AE是∠BAC的平分线,∠ABC的平分线 BM交AE于点M,点O在AB上,以点O为圆心,OB的长为半径的圆经过点M,交BC于点G,交 AB于点F.
如图,在△ABC中,AB=AC,AE是∠BAC的平分线,∠ABC的平分线 BM交AE于点M,点O在AB上,以点O为圆心,OB的长为半径的圆经过点M,交BC于点G,交 AB于点F.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1-a>1-b | B. | $\frac{1}{a}<\frac{1}{b}$ | C. | $\frac{a}{b}<1$ | D. | $-\frac{1}{3}a>-\frac{1}{3}b$. |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
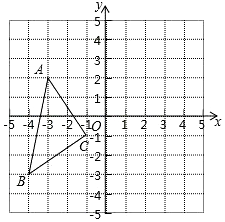 如图所示,写出△ABC各顶点的坐标以及△ABC关于x对称的△A1B1C1的各顶点坐标,并画出△ABC关于y对称的△A2B2C2.并求△ABC的面积.
如图所示,写出△ABC各顶点的坐标以及△ABC关于x对称的△A1B1C1的各顶点坐标,并画出△ABC关于y对称的△A2B2C2.并求△ABC的面积.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com