
����Ŀ����֪OABC�Ķ���A��C�ֱ���ֱ��x=2��x=4�ϣ�OΪ����ԭ�㣬ֱ��x=2�ֱ���x���OC�߽���D��E��ֱ��x=4�ֱ���x���AB�ߵĽ��ڵ�F��G��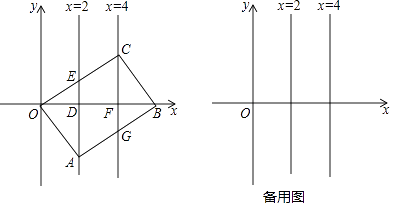
��1����ͼ���ڵ�A��C�ƶ��Ĺ����У�����B��x���ϣ�
��ֱ�� AC�Ƿ�ᾭ��һ�����㣬���ǣ���ֱ��д����������ꣻ������˵�����ɣ�
��OABC�Ƿ�����γɾ��Σ�������ԣ����������OABC�������������˵�����ɣ�
���ı���AECG�Ƿ�����γ����Σ�������ԣ����������AECG�������������˵�����ɣ�
��2���ڵ�A��C�ƶ��Ĺ����У�����B����x���ϣ��ҵ�OABCΪ������ʱ��ֱ��д����C�����꣮
���𰸡�
��1��
�⣺���ǣ��������㣨3��0�����������£�
��ͼ1�У�����AC��OB��K��
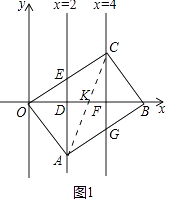
���ı���OABC��ƽ���ı��Σ�
��OK=KB��BC��OA��BC=OA��
���CBF=��AOD��
�ڡ�DOA�͡�FBC�У�
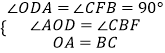 ��
��
���DOA�ա�FBC��
��OD=FB=2��
��OB=6��
��OK=KB��
��OK=3��
��K��3��0����
��ֱ��AC��������K��3��0����
�ڿ��ԣ��������£�
����OCB=90��ʱ���ı���OABC�Ǿ��Σ�
�ɣ�1����֪��DOA�ա�FBC��
��OD=BF=2��
�ߡ�OCF+��FCB=90�㣬��FCB+��CBF=90�㣬
���OCF=��CBF��
�ߡ�CFO=��CFB��
���CFO�ס�BFC��
�� ![]() =
= ![]() ��
��
�� ![]() =
= ![]() ��
��
��CF=2 ![]() ��
��
��S����OABC=2S��OBC=2�� ![]() ��
�� ![]() =12
=12 ![]() ��
��
�ۿ��ԣ��������£�
��ͼ3�У���֪��OE=EC=AEʱ���ı���AECG�����Σ�
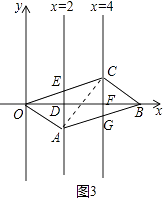
�ɣ�1����֪����DOA�ա�FBC��
��AD=CF��
��DE= ![]() CF����DE=x����AD=CF=2x��OE=AE=3x��
CF����DE=x����AD=CF=2x��OE=AE=3x��
��Rt��ADE����OE2=OD2+DE2��
��9x2=x2+4��
��x= ![]() ��
��
��AE= ![]() ��
��
��S����AECG=AEDF= ![]() ��2=3
��2=3 ![]()
��2��
�⣺��ͼ4�У�
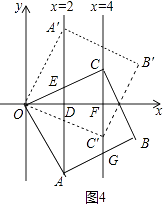
���ı���OABC��������ʱ����֤��DOA�ա�FCO��
��OD=CF=2��
���C���꣨4��2����
���ݶԳ���C�䣨4����2��ʱ��Ҳ����������
������������C������4��2����4����2��
����������1�����ǣ��������㣨3��0������ͼ1�У�����AC��OB��K��ֻҪ֤��OD=FB=2���Ƴ�OB=6�����ɽ�����⣮�ڵ���OCB=90��ʱ���ı���OABC�Ǿ��Σ��ɣ�1����֪��DOA�ա�FBC���Ƴ�OD=BF=2���ɡ�CFO�ס�BFC���ɵ� ![]() =
= ![]() ���ɴ˼��ɽ�����⣮�ۿ��ԣ���ͼ3�У���֪��OE=EC=AEʱ���ı���AECG�����Σ��ɣ�1����֪����DOA�ա�FBC���Ƴ�AD=CF����֪DE=
���ɴ˼��ɽ�����⣮�ۿ��ԣ���ͼ3�У���֪��OE=EC=AEʱ���ı���AECG�����Σ��ɣ�1����֪����DOA�ա�FBC���Ƴ�AD=CF����֪DE= ![]() CF����DE=x����AD=CF=2x��OE=AE=3x����Rt��ADE�У�����OE2=OD2+DE2 �� �г����̼��ɽ�����⣮��2����ͼ4�У����ı���OABC��������ʱ����֤��DOA�ա�FCO���Ƴ�OD=CF=2���Ƴ���C���꣨4��2�������ݶԳ���C�䣨4����2��ʱ��Ҳ����������
CF����DE=x����AD=CF=2x��OE=AE=3x����Rt��ADE�У�����OE2=OD2+DE2 �� �г����̼��ɽ�����⣮��2����ͼ4�У����ı���OABC��������ʱ����֤��DOA�ա�FCO���Ƴ�OD=CF=2���Ƴ���C���꣨4��2�������ݶԳ���C�䣨4����2��ʱ��Ҳ����������
�����㾫�����������⣬������Ҫ�˽����ε�����(���ε������߶���ȣ����εĶԽ����ഹֱ������ÿһ���Խ���ƽ��һ��Խǣ����α������Խ��߷ֳ��ĸ�ȫ�ȵ�ֱ�������Σ����ε�������������Խ��߳��Ļ���һ��)����Ҫ���վ��ε�����(���ε��ĸ��Ƕ���ֱ�ǣ����εĶԽ������)�����֪ʶ���Ǵ���Ĺؼ���


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ������˿͵�����ij�̳���5kg���ǣ�3kg�����Ǻ�2kgˮ���ǻ�ϳ�ʲ���dz��ۣ���֪���ǵ��ۼ�Ϊÿǧ��40Ԫ��������Ϊÿǧ��20Ԫ��ˮ����Ϊÿǧ��15Ԫ����Ϻ�ʲ���ǵ��ۼ�ӦΪÿǧ�ˣ� ��
A.25Ԫ
B.28.5Ԫ
C.29Ԫ
D.34.5Ԫ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2011�꣬����ͳ�ƾֹ����˵�����ȫ���˿��ղ��������˿�ԼΪ1339700000�ˣ���1339700000�ÿ�ѧ��������ʾ��ȷ���ǣ� ��
A.0.13397��1010
B.1.3397��109
C.13.397��108
D.13397��105
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ʵ����ѧ�涨ѧ��ѧ�ڵ���ѧ�ɼ�����Ϊ120�֣�����ƽʱ�ɼ�ռ20%�����п��Գɼ�ռ30%����ĩ���Գɼ�ռ50%�����������ɼ�������100�֣�90�֣�106�֣���ô������ѧ�ڵ���ѧ�ɼ�Ϊ_____�֣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����м�����ȷ���ǣ� ��
A.3m��m=2
B.m4��m3=m
C.����m2��3=m6
D.����m��n��=m+n
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y=x2����2k+1��x+k2+k��k��0��
��1����k=![]() ʱ����������κ����Ľ���ʽд�ɶ���ʽ��
ʱ����������κ����Ľ���ʽд�ɶ���ʽ��
��2����֤������x��һԪ���η���x2����2k+1��x+k2+k=0����������ȵ�ʵ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ա߳�Ϊ2�������ε�����OΪ�˵㣬���������ֱ�����ߣ��ֱ��������εı߽���A��B���㣬���߶�AB��ȡֵ��Χ�� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������֪������ʽ�ͷ������źܶ�����Ƶ㣮����ȷ����Ļ������ʣ����ǵõ��˷�ʽ�Ļ������ʣ���ȷ��������㷨�����ǵõ��˷�ʽ�����㷨�ȵȣ�Сѧ��ѷ��ӱȷ�ĸС�ķ�����������������Ƶأ����ǰѷ�����ʽ�Ĵ���С�ڷ�ĸ��ʽ�Ĵ����ķ�ʽ��Ϊ���ʽ����֮����Ϊ�ٷ�ʽ�������κ�һ���ٷ�ʽ�����Ի�����ʽ�����ʽ�ĺ͵���ʽ�� �磺 ![]() =
= ![]() =
= ![]() +
+ ![]() =1+
=1+ ![]() ��
��![]() =
= ![]() =
= ![]() +
+ ![]() =2+����
=2+���� ![]() ����
����
��1�����з�ʽ�У��������ʽ���ǣ�������ţ��� �� ![]()
�� ![]()
�� ![]()
�� ![]()
��2�����ٷ�ʽ ![]() ������ʽ�����ʽ�ĺ͵���ʽΪ��
������ʽ�����ʽ�ĺ͵���ʽΪ�� ![]() =+ �� ���ٷ�ʽ
=+ �� ���ٷ�ʽ ![]() ��ֵΪ��������������a��ֵΪ��
��ֵΪ��������������a��ֵΪ��
��3�����ٷ�ʽ ![]() ������ʽ�����ʽ�ĺ͵���ʽ��
������ʽ�����ʽ�ĺ͵���ʽ�� ![]() = ��
= ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ھ���ABCD�У�AB��1��AD��![]() ��AFƽ�֡�DAB����C����CE��BD��E���ӳ�AF.EC���ڵ�H�����н����У���AF��FH����BO��BF����CA��CH����BE��3ED����ȷ���ǣ�������
��AFƽ�֡�DAB����C����CE��BD��E���ӳ�AF.EC���ڵ�H�����н����У���AF��FH����BO��BF����CA��CH����BE��3ED����ȷ���ǣ�������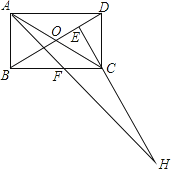
A.�ڢ�
B.�ۢ�
C.�٢ڢ�
D.�ڢۢ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com