
 如图的三角形纸片中,AB=AC,BC=12cm,∠C=30°,折叠这个三角形,使点B落在AC的中点D处,折痕为EF,那么BF的长为$\frac{14}{3}$cm.
如图的三角形纸片中,AB=AC,BC=12cm,∠C=30°,折叠这个三角形,使点B落在AC的中点D处,折痕为EF,那么BF的长为$\frac{14}{3}$cm. 分析 首先过D作DH⊥BC,过点A作AN⊥BC于点N,根据题意结合等腰三角形的性质进而得出CN的长,再利用锐角三角函数关系以及勾股定理得出答案.
解答 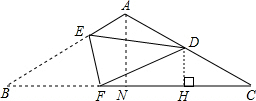 解:过D作DH⊥BC,过点A作AN⊥BC于点N,
解:过D作DH⊥BC,过点A作AN⊥BC于点N,
∵AB=AC,
∴∠B=∠C=30°,
根据折叠可得:DF=BF,∠EDF=∠B=30°,
∵AB=AC,BC=12cm,
∴BN=NC=6cm,
∵点B落在AC的中点D处,AN∥DH,
∴NH=HC=3cm,
∴DH=3•tan30°=$\sqrt{3}$(cm),
设BF=DF=xcm,则FH=12-x-3=9-x(cm),
故在Rt△DFH中,DF2=DH2+FH2,
故x2=($\sqrt{3}$)2+(9-x)2,
解得:x=$\frac{14}{3}$,
即BF的长为:$\frac{14}{3}$cm.
故答案为:$\frac{14}{3}$.
点评 此题主要考查了翻折变换以及勾股定理、等腰三角形的性质等知识,正确得出DH的长是解题关键.


 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:初中数学 来源: 题型:选择题
 小李同学掷一枚质地均匀的骰子,点数为2的一面朝上的概率为( )
小李同学掷一枚质地均匀的骰子,点数为2的一面朝上的概率为( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{5}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 在某中学抽取200名女生 | |
| B. | 在某中学抽取200名男生 | |
| C. | 在某中学抽取200名学生 | |
| D. | 在河池市中学生中随机抽取200名学生 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-2,3) | B. | (-3,2) | C. | (2,-3) | D. | (3,-2) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 测试项目 | 测试成绩/分 | ||
| 甲 | 乙 | 丙 | |
| 笔试 | 80 | 90 | 90 |
| 面试 | 100 | 70 | 80 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com