
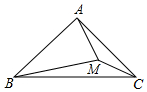
 如图,在△ABC中,∠BAC=90°,AB=AC,M为△ABC内一点,恰好满足BA=BM,AM=CM,则∠ABM的度数为30°.
如图,在△ABC中,∠BAC=90°,AB=AC,M为△ABC内一点,恰好满足BA=BM,AM=CM,则∠ABM的度数为30°. 分析 作MD⊥AC于点D,ME⊥AB于点E.先依据等腰三角形三线合一的性质证明AD=$\frac{1}{2}$AC,然后再证明四边形ADME是矩形,从而可得到EM=$\frac{1}{2}$AC,由AC=AB=BM可得到ME=$\frac{1}{2}$BM,最后,依据特殊锐角三角函数值求解即可.
解答 解:作MD⊥AC于点D,ME⊥AB于点E.
∵MA=MC,MD⊥AC,
∴AD=CD.
∵∠AEM=∠BAC=∠MDA=90°
∴四边形ADME是矩形
∴ME=AD=$\frac{1}{2}$AC
∵AB=AC=BM
∴ME=AD=$\frac{1}{2}$AC=$\frac{1}{2}$AB=$\frac{1}{2}$BM.
∴∠ABM=30°.
点评 本题主要考查的是等腰三角形的性质、矩形的判定和性质、特殊锐角三角函数值的应用,证得ME=$\frac{1}{2}$BM是解题的关键.


 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
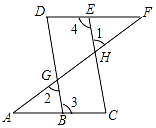 如图,点E在直线DF上,点B在直线AC上,若∠1=∠2,∠3=∠4,求证:∠A=∠F
如图,点E在直线DF上,点B在直线AC上,若∠1=∠2,∠3=∠4,求证:∠A=∠F 查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
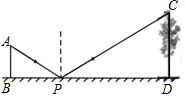 如图是小王同学设计的测量树高的示意图.在点P处放一水平的平面镜,小王同学站在地面的B处,通过平面镜刚好能看见大树CD的顶端C,若小王身高AB=1.6米,BP=3米,PD=15米,则大树的高度CD是8米.
如图是小王同学设计的测量树高的示意图.在点P处放一水平的平面镜,小王同学站在地面的B处,通过平面镜刚好能看见大树CD的顶端C,若小王身高AB=1.6米,BP=3米,PD=15米,则大树的高度CD是8米.查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 38 | B. | 44 | C. | 65 | D. | 73 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com