

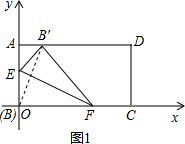
 解:(1)如图1,∵将矩形折叠,使B落在边AD(含端点)上,落点记为B′,
解:(1)如图1,∵将矩形折叠,使B落在边AD(含端点)上,落点记为B′, =8,
=8,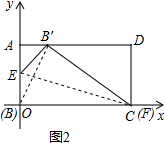
 ,
, ×BE×AB′=
×BE×AB′= ×
× ×2=
×2= ,
,

科目:初中数学 来源: 题型:
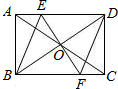 4、如图,已知矩形ABCD中(AD>AB),EF经过对角线的交点O,且分别交AD,BC于E,F,请你添加一个条件:
4、如图,已知矩形ABCD中(AD>AB),EF经过对角线的交点O,且分别交AD,BC于E,F,请你添加一个条件:查看答案和解析>>
科目:初中数学 来源:浙江省杭州市2011-2012学年九年级下学期教学检测数学试题 题型:044
已知矩形ABCD如图放置,将矩形折叠,使B落在边AD(含端点)上,落点记为![]() ,折痕与线段AB交于E,与边BC或者边CD(含端点)交于F,则以E、B、
,折痕与线段AB交于E,与边BC或者边CD(含端点)交于F,则以E、B、![]() 为顶点的三角形ΔBB/E称为矩形ABCD的“折叠三角形”.
为顶点的三角形ΔBB/E称为矩形ABCD的“折叠三角形”.
(1)由折叠三角形定义可知,矩形ABCD的任意一个折叠ΔBEB/都是一个________三角形.
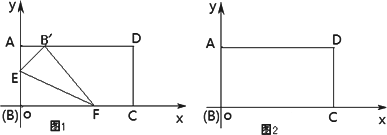
(2)在矩形ABCD中,AB=6,AD=10,当F与点C重合时,在下图中画出这个折叠ΔBE![]() ,试求点B/的坐标并求这个折叠ΔBE
,试求点B/的坐标并求这个折叠ΔBE![]() 的面积.
的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com