
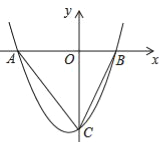
【题目】如图,抛物线y=ax2+bx﹣5(a≠0)与x轴交于点A(﹣5,0)和点B(3,0),与y轴交于点C.
(1)求该抛物线的解析式;
(2)若点E为x轴下方抛物线上的一动点,当S△ABE=S△ABC时,求点E的坐标;
(3)在(2)的条件下,抛物线上是否存在点P,使∠BAP=∠CAE?若存在,求出点P的横坐标;若不存在,请说明理由.
【答案】(1)y=![]() x2+
x2+![]() x﹣5;(2)E点坐标为(﹣2,﹣5);(3)存在满足条件的点P,其横坐标为
x﹣5;(2)E点坐标为(﹣2,﹣5);(3)存在满足条件的点P,其横坐标为![]() 或
或![]() .
.
【解析】
试题分析:(1)把A、B两点的坐标代入,利用待定系数法可求得抛物线的解析式;(2)当S△ABE=S△ABC时,可知E点和C点的纵坐标相同,可求得E点坐标;(3)在△CAE中,过E作ED⊥AC于点D,可求得ED和AD的长度,设出点P坐标,过P作PQ⊥x轴于点Q,由条件可知△EDA∽△PQA,利用相似三角形的对应边可得到关于P点坐标的方程,可求得P点坐标.
试题解析:(1)把A、B两点坐标代入解析式可得![]() ,解得
,解得![]() ,
,
∴抛物线解析式为y=![]() x2+
x2+![]() x﹣5;
x﹣5;
(2)在y=![]() x2+
x2+![]() x﹣5中,令x=0可得y=﹣5,
x﹣5中,令x=0可得y=﹣5,
∴C(0,﹣5),
∵S△ABE=S△ABC,且E点在x轴下方,
∴E点纵坐标和C点纵坐标相同,
当y=﹣5时,代入可得![]() x2+
x2+![]() x=﹣5,解得x=﹣2或x=0(舍去),
x=﹣5,解得x=﹣2或x=0(舍去),
∴E点坐标为(﹣2,﹣5);
(3)假设存在满足条件的P点,其坐标为(m,![]() m2+
m2+![]() m﹣5),
m﹣5),
如图,连接AP、CE、AE,过E作ED⊥AC于点D,过P作PQ⊥x轴于点Q,
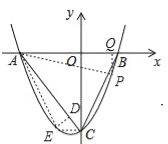
则AQ=AO+OQ=5+m,PQ=|![]() m2+
m2+![]() m﹣5|,
m﹣5|,
在Rt△AOC中,OA=OC=5,则AC=5![]() ,∠ACO=∠DCE=45°,
,∠ACO=∠DCE=45°,
由(2)可得EC=2,在Rt△EDC中,可得DE=DC=![]() ,
,
∴AD=AC﹣DC=5![]() ﹣
﹣![]() =4
=4![]() ,
,
当∠BAP=∠CAE时,则△EDA∽△PQA,
∴![]() ,即
,即![]() =
=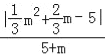 ,
,
∴![]() m2+
m2+![]() m﹣5=
m﹣5=![]() (5+m)或
(5+m)或![]() m2+
m2+![]() m﹣5=﹣
m﹣5=﹣![]() (5+m),
(5+m),
当![]() m2+
m2+![]() m﹣5=
m﹣5=![]() (5+m)时,整理可得4m2﹣5m﹣75=0,解得m=
(5+m)时,整理可得4m2﹣5m﹣75=0,解得m=![]() 或m=﹣5(与A点重合,舍去),
或m=﹣5(与A点重合,舍去),
当![]() m2+
m2+![]() m﹣5=﹣
m﹣5=﹣![]() (5+m)时,整理可得4m2+11m﹣45=0,解得m=
(5+m)时,整理可得4m2+11m﹣45=0,解得m=![]() 或m=﹣5(与A点重合,舍去),
或m=﹣5(与A点重合,舍去),
∴存在满足条件的点P,其横坐标为![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】下列命题是真命题的是( )
A.菱形的对角线相等B.对角线互相垂直的平行四边形是正方形
C.三个角都相等的四边形是矩形D.对角线相等的平行四边形是矩形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】人体中红细胞的直径约为0.0000077m,将0.0000077用科学记数法表示为( )
A.7.7×10﹣5
B.7.7×10﹣6
C.77×10﹣7
D.0.77×10﹣5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 一个数的绝对值一定比0大 B. 倒数等于它本身的数是±1
C. 绝对值等于它本身的数一定是正数 D. 一个数的相反数一定比它本身小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】体育文化用品商店购进篮球和排球共20个,进价和售价如下表,全部销售完后共获利润260元.
篮球 | 排球 | |
进价(元/个) | 80 | 50 |
售价(元/个) | 95 | 60 |
求:(1)购进篮球和排球各多少个?
(2)销售6个排球的利润与销售几个篮球的利润相等?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com