
����Ŀ�������п�չ����������У�Ϊ����ѧ�����չ�����������ȫ�а��꼶����ͬѧ1���ӣ�����������У�����������������ͼ�������ͼ���ṩ��Ϣ��������⣺
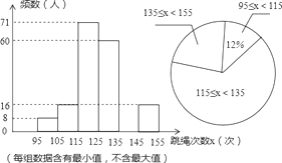
��1�����ι���������ѧ����
��2���벹ȫֱ��ͼ��ȱ���֣�ֱ��д����ͼ�з�Χ135��x��155��������Բ�ĽǶ�����
��3�������γ���У���125�����ϣ���125�Σ�Ϊ���㣬�������ȫ��8000�����꼶ѧ�����ж�����ѧ���ɼ�Ϊ���㣿
��4���������������Ϣ�������п�չѧ���̸̸�Լ���������
���𰸡���1��200�ˣ���2��81�㣻��3��4200�ˣ���4��������
�������������������1������95��x��115��������8+16=24�ˣ���ռ�ı�����12%������⣻
��2����÷�Χ��135��x��145�����������ε�Բ�ĽǶ�����360�ȳ��Զ�Ӧ�ı���������⣻
��3�����������ռ�ı�����Ȼ�����������8000������⣻
��4������ʵ�����������Լ��ļ��⼴�ɣ��𰸲�Ψһ��
�����������1����������������8+16����12%=200���ˣ���
��2����Χ��135��x��145�������ǣ�200-8-16-71-60-16=29���ˣ���
������������Χ135��x��155�������ε�Բ�ĽǶ����ǣ�360��![]() =81����
=81����
��3������ı����ǣ� ![]() ��100%=52.5%�������ȫ��8000�����꼶ѧ�����ж�����ѧ���ijɼ�Ϊ���������ǣ�8000��52.5%=4200���ˣ���
��100%=52.5%�������ȫ��8000�����꼶ѧ�����ж�����ѧ���ijɼ�Ϊ���������ǣ�8000��52.5%=4200���ˣ���
��4��ȫ�дﵽ�����������һ�����ϣ���ӳ������ѧ����������ܺ�.�𰸲�Ψһ


 ������������Ծ�ϵ�д�
������������Ծ�ϵ�д� �������Ӳ�ϵ�д�
�������Ӳ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵����ȷ���ǣ� ��
A.����һ�ŵ�ӰƱ����λ��Ϊż�����DZ�Ȼ�¼�
B.���ס����������ݵķ���ֱ�Ϊs ![]() =0.3��s
=0.3��s ![]() =0.1����������ݱ����������ȶ�
=0.1����������ݱ����������ȶ�
C.һ������2��4��5��5��3��6��������5
D.��ij�齱����н���Ϊ ![]() ����μ�6�γ齱һ����1�����н�
����μ�6�γ齱һ����1�����н�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��A��BΪ����������![]() ͼ���ϵ����㣬A��B��������ֱ�Ϊ��
ͼ���ϵ����㣬A��B��������ֱ�Ϊ��![]() ������
������![]() ����m��n��������AB���ӳ���
����m��n��������AB���ӳ���![]() ���ڵ�C.
���ڵ�C.
��1����![]() ��ֵ��
��ֵ��
��2����BΪAC���е㣬��![]() ��ֵ��
��ֵ��
��3����B����OA��ƽ���߽�![]() ���ڣ�
���ڣ�![]() ��0������
��0������![]() ��������
Ϊ��������![]() ֵ.
ֵ.
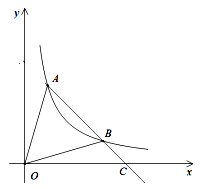
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�OΪ����ԭ�㣬��֪��F��2 ![]() ��0����ֱ��GF��y���������ڵ�G���ҡ�GFO=30�㣮
��0����ֱ��GF��y���������ڵ�G���ҡ�GFO=30�㣮 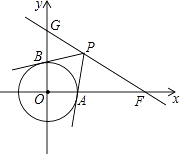
��1����ֱ��д����G�����ꣻ
��2������O�İ뾶Ϊ1����P��ֱ��GF�ϵĶ��㣬ֱ��PA��PB�ֱ����O�����ڵ�A��B��
�������߳�PB����Сֵ��
����ֱ��GF���Ƿ���ڵ�P��ʹ�á�APB=60�㣿�����ڣ��������P�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(����10��)Ϊ�˽���꼶ѧ���Ŀ����Ķ��������У������Ӱ��꼶�����ȡ��������ѧ���������ǵĶ���ʱ������˵��鲢���ռ������ݻ����������������ͳ��ͼ����������ͼ���ṩ����Ϣ������������⣺��ÿ�麬��Сֵ�������ֵ��
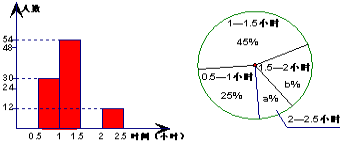
��1�����Ӱ��꼶��ȡ�˶�����ѧ����
��2������� (ֱ�ӰѴ��������)
�١�2��2.5Сʱ���IJ��ֶ�Ӧ������Բ�Ľ�Ϊ_______�ȣ�
�������Ķ�ʱ�����λ������________(��ʱ���)�ڣ�
��3����������꼶����800��ѧ�����������꼶ѧ�������Ķ�ʱ��
������1.5Сʱ���ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1�����뾶Ϊ2��Բ��ֽƬ��Բ���������ഹֱ��ֱ��AC,BD�����۵��õ���ͼ2��ʾ������OAB��Ȼ������OB���д���EF������OAB�������������֣����OEF=�㣻�ұ߲��־�������չ����ѹƽ�����õ�ͼ�ε��ܳ�Ϊ 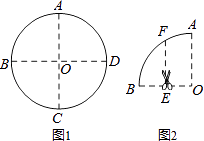
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
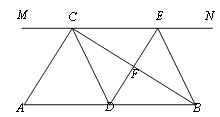
����Ŀ����ͼ����Rt��ABC�У���ACB��90�㣬����C��ֱ��MN��AB��DΪAB����һ�㣬����D��DE��BC����ֱ��MN��E������ΪF������CD��BE��
��1����֤��CE��AD��
��2����D��AB�е�ʱ��
����֤���ı���BECD�����Σ�
�ڵ���AΪ���ٶ�ʱ���ı���BECD�������Σ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ϵ�з���һ����OABC����֪��ABC=60����OA=1���Ƚ�����OABC��x���������������ת��ÿ�η�ת60����������ת2014�Σ���B���������ΪB1��B2��B3��������B2014������Ϊ ��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com