
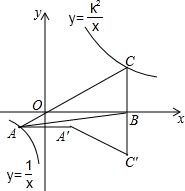
 如图,已知在平面直角坐标系xOy中,O是坐标原点,点A是函数y=$\frac{1}{x}$(x<0)图象上一点,AO的延长线交函数y=$\frac{k^2}{x}$(x>0,k>0的常数)的图象于点C,点A关于y轴的对称点为A′,点C关于x轴的对称点为C′且点O、A′、C′在同一条直线上,连接CC′,交x轴于点B,连接AB,AA′,A′C′,若△ABC的面积等于6,则由线段AC,CC′,C′A′,A′A所围成的图形的面积等于10.
如图,已知在平面直角坐标系xOy中,O是坐标原点,点A是函数y=$\frac{1}{x}$(x<0)图象上一点,AO的延长线交函数y=$\frac{k^2}{x}$(x>0,k>0的常数)的图象于点C,点A关于y轴的对称点为A′,点C关于x轴的对称点为C′且点O、A′、C′在同一条直线上,连接CC′,交x轴于点B,连接AB,AA′,A′C′,若△ABC的面积等于6,则由线段AC,CC′,C′A′,A′A所围成的图形的面积等于10. 分析 过A作AD⊥x轴于D,连接OA′,设A(a,$\frac{1}{a}$),C(b,$\frac{{k}^{2}}{b}$),由△OAD∽△BCO,得到$\frac{{S}_{△ADO}}{{S}_{△BCO}}$=($\frac{OD}{OB}$)2=$\frac{{a}^{2}}{{b}^{2}}$,根据反比例函数的系数k的几何意义得到S△ADO=$\frac{1}{2}$,S△BOC=$\frac{{k}^{2}}{2}$,求出k2=($\frac{b}{a}$)2,得到k=-$\frac{b}{a}$,根据S△ABC=S△AOB+S△BOC=$\frac{1}{2}$(-$\frac{1}{a}$)•b+$\frac{{k}^{2}}{2}$=6,列出关于k的方程k2+k-12=0,求得k=3,由于点A关于y轴的对称点为A′,点C关于x轴的对称点为C′,得到OA′,OC′在同一条直线上,于是得到由线段AC,CC′,C′A′,A′A所围成的图形的面积=S△OBC+S△OBC′+S△OAA′=10.
解答 解:过A作AD⊥x轴于D,连接OA′,
∵点A是函数y=$\frac{1}{x}$(x<0)图象上一点,
∴设A(a,$\frac{1}{a}$),
∵点C在函数y=$\frac{{k}^{2}}{x}$(x>0,k是不等于0的常数)的图象上,
∴设C(b,$\frac{{k}^{2}}{b}$),
∵AD⊥BD,BC⊥BD,
∴△OAD∽△BCO,
∴$\frac{{S}_{△ADO}}{{S}_{△BCO}}$=($\frac{OD}{OB}$)2=$\frac{{a}^{2}}{{b}^{2}}$,
∵S△ADO=$\frac{1}{2}$,S△BOC=$\frac{{k}^{2}}{2}$,
∴k2=($\frac{b}{a}$)2,
∵S△ABC=S△AOB+S△BOC=$\frac{1}{2}$(-$\frac{1}{a}$)•b+$\frac{{k}^{2}}{2}$=6,
∴k2-$\frac{b}{a}$=12,
①当k>0时,
k=-$\frac{b}{a}$,
∴k2+k-12=0,
解得:k=3,k=-4(不合题意舍去),
②当k<0时,
k=$\frac{b}{a}$,
∴k2+k-12=0,
解得:k=-3,k=4(不合题意舍去),
∴k2=9
∵点A关于y轴的对称点为A′,点C关于x轴的对称点为C′,
∴∠1=∠2,∠3=∠4,
∴∠1+∠4=∠2+∠3=90°,
∴OA′,OC′在同一条直线上,
∴S△OBC′=S△OBC=$\frac{{k}^{2}}{2}$=$\frac{9}{2}$,
∵S△OAA′=2S△OAD=1,
∴由线段AC,CC′,C′A′,A′A所围成的图形的面积=S△OBC+S△OBC′+S△OAA′=10.
故答案为:10.
点评 本题考查了反比例函数的图象的性质,系数k的几何意义,相似三角形的判定和性质,轴对称的性质,正确的理解轴对称图形的性质是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
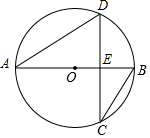 如图,AB为⊙O的直径,弦DC垂直AB于点E,∠DCB=30°,EB=3,则弦AC的长度为( )
如图,AB为⊙O的直径,弦DC垂直AB于点E,∠DCB=30°,EB=3,则弦AC的长度为( )| A. | 3$\sqrt{3}$ | B. | $4\sqrt{3}$ | C. | $5\sqrt{3}$ | D. | $6\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{a+b}{2}$元 | B. | (am+bn)%元 | C. | $\frac{am+bn}{a+b}$元 | D. | $\frac{am+bn}{m+n}$元 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某中学教学楼的后面靠近一座山坡,坡面下是一块草地,如图所示,BC∥AD,斜坡AB=160米,坡度i=$\sqrt{3}$:1,为防止山体滑坡,保障学生安全,学校决定不仅加固教学楼,还对山坡进行改造,当坡角不超过45°时可保证山体不滑坡,改造时保持坡脚A不动,从坡顶B沿BC进到E处,问BE至少是多少米?(结果保留根号)
某中学教学楼的后面靠近一座山坡,坡面下是一块草地,如图所示,BC∥AD,斜坡AB=160米,坡度i=$\sqrt{3}$:1,为防止山体滑坡,保障学生安全,学校决定不仅加固教学楼,还对山坡进行改造,当坡角不超过45°时可保证山体不滑坡,改造时保持坡脚A不动,从坡顶B沿BC进到E处,问BE至少是多少米?(结果保留根号)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com