
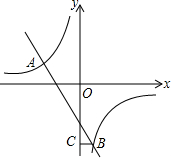
 如图,在平面直角坐标系中,双曲线y=
如图,在平面直角坐标系中,双曲线y=| m |
| x |
| m |
| x |
| m |
| x |
| m |
| -3 |
| 6 |
| x |
| 6 |
| x |
| 6 |
| a |
|
|
| 1 |
| 2 |
| 1 |
| 2 |


科目:初中数学 来源: 题型:
| 椪柑品种 | A | B | C |
| 每辆汽车运载量(吨) | 10 | 8 | 6 |
| 每吨椪柑获利(元) | 800 | 1200 | 1000 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| b |
| a |
| c |
| a |
| pq+1 |
| q |
| 1 |
| q |
| 1 |
| q |
| 1 |
| q |
| 1 |
| q |
| 1 |
| q |
| pq+1 |
| q |
| 1 |
| p2 |
| 1 |
| p |
| 1 |
| q2 |
| 1 |
| q |
| 1 |
| p |
| 1 |
| q |
| 1 |
| n2 |
| 5 |
| n |
| 1 |
| m |
| 1 |
| n |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,排球运动员站在点O处练习发球,将球从点O正上方2米的点A处发出把球看成点,其运行的高度y(米)与运行的水平距离x(米)满足关系式y=a(x-6)2+h,已知球网与点O的水平距离为9米,高度为2.43米,球场的边界距点O的水平距离为18米.
如图,排球运动员站在点O处练习发球,将球从点O正上方2米的点A处发出把球看成点,其运行的高度y(米)与运行的水平距离x(米)满足关系式y=a(x-6)2+h,已知球网与点O的水平距离为9米,高度为2.43米,球场的边界距点O的水平距离为18米.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com