

���� ��1����֪���������Լ��������ϵĵ㣨3��0�������ô���ϵ����������ú�������ʽ��
��2���������ô���ϵ�������AC�Ľ���ʽ����P�ĺ�������m������m���Ա�ʾ����ACG����������ú������������P�����ꣻ
��3���������G�����꣬Ȼ����GH��AC�ڵ�H�����AH��GH�ij��ȣ�Ȼ�����OD�ij����������������ε����ʼ��ɽ��
��� �⣺��1���������ߵĽ���ʽ��y=a��x-1��2+4��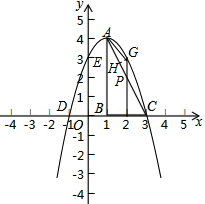
�ѣ�3��0������ã�4a+4=0��
��ã�a=-1��
�������ߵĽ���ʽ��y=-��x-1��2+4����y=-x2+2x+3��
��2����AC�Ľ���ʽ��y=kx+b����������ã�$\left\{\begin{array}{l}{k+b=4}\\{3k+b=0}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{k=-2}\\{b=6}\end{array}\right.$��
��AC�Ľ���ʽ��y=-2x+6��
��P�������ǣ�m��-2m+6����
��S=$\frac{1}{2}$��2����-m2+2m+3+2m-6��=-m2+4m-3��
��m=2ʱ��S�����ֵ��
��x=2ʱ��y=-4+6=2����P�������ǣ�2��2����
��3����x=2����y=-x2+2x+3��y=-4+4+3=3��
��G�������ǣ�2��3����
�辭��G�Ҵ�ֱ��AC��ֱ�ߵĽ���ʽ��y=$\frac{1}{2}$x+c���ѣ�2��3�������1+c=3��
��ã�c=2��
��G�Ҵ�ֱ��AC��ֱ��HG�Ľ���ʽ��y=$\frac{1}{2}$x+2��
��������ã�$\left\{\begin{array}{l}{y=\frac{1}{2}x+2}\\{y=-2x+6}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{x=\frac{8}{5}}\\{y=\frac{14}{5}}\end{array}\right.$��
��H�������ǣ�$\frac{8}{5}$��$\frac{14}{5}$����
��QH=$\sqrt{��2-\frac{8}{5}��^{2}+��3-\frac{14}{5}��^{2}}$=$\frac{\sqrt{5}}{5}$��AH=$\sqrt{��\frac{8}{5}-1��^{2}+��4-\frac{14}{5}��^{2}}$=$\frac{3\sqrt{5}}{5}$��
��AH��HQ=3��1��
C��3��0������x=1�ĶԳƵ��ǣ�-1��0��������x����һ����D�������ǣ�-1��������OD=1��
������y=-x2+2x+3�У���x=0ʱ��y=3������������y��Ľ����ǣ�0��3����OE=3��
��OE��OD=3��1��
��Q��0��3��ʱ����ODE�ס�HQA����ʱ��GAP+��QDO=90�㣻
E����x��ĶԳƵ�E���ǣ�0��-3����
��ֱ��DE��Ľ���ʽ��y=mx+n��
��$\left\{\begin{array}{l}{-m+n=0}\\{n=-3}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{m=-3}\\{n=-3}\end{array}\right.$��
��ֱ��DE��Ľ���ʽ��y=-3x-3��
��������ã�$\left\{\begin{array}{l}{y=-{x}^{2}+2x+3}\\{y=-3x-3}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{x=6}\\{y=-2}\end{array}\right.$��
��Q�������ǣ�6��-2����
��֮��Q�������ǣ�0��3����6��-2����
���� ���⿼���˴���ϵ������������ʽ�Լ����������ε��ж������ʣ�ע�����Q����������y��Ľ���ʱ�����GAP+��QDO=90���ǹؼ���


 ����С��ʿ���������ϵ�д�
����С��ʿ���������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2��3��5 | B�� | 4��5��6 | C�� | 11��12��15 | D�� | 8��15��17 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����Rt��ABC�У���BAC=90�㣬AC=2AB����D��AC���е㣬��һ�����Ϊ45������ǰ���ͼ���ã�ʹ���ǰ�б�ߵ������˵�ֱ���A��D�غϣ�E��ֱ�Ƕ��㣬����EC��BE����֤��BE=CE��
��ͼ����Rt��ABC�У���BAC=90�㣬AC=2AB����D��AC���е㣬��һ�����Ϊ45������ǰ���ͼ���ã�ʹ���ǰ�б�ߵ������˵�ֱ���A��D�غϣ�E��ֱ�Ƕ��㣬����EC��BE����֤��BE=CE���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ����֪��ABC�͡�DCE���ǵȱ������Σ���B��C��E��ͬ��ֱ���ϣ�AE��BD���ڵ�O��AE��CD�ཻ�ڵ�G��AC��BD���ڵ�F������0C��FG�������н��ۣ���AE=BD����AG=BF����FG��BE���ܡ�BOA=60�㣬������ȷ���У�������
��ͼ����֪��ABC�͡�DCE���ǵȱ������Σ���B��C��E��ͬ��ֱ���ϣ�AE��BD���ڵ�O��AE��CD�ཻ�ڵ�G��AC��BD���ڵ�F������0C��FG�������н��ۣ���AE=BD����AG=BF����FG��BE���ܡ�BOA=60�㣬������ȷ���У�������| A�� | 1�� | B�� | 2�� | C�� | 3�� | D�� | 4�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com