
【题目】在⊙O中,AB为⊙O的直径,AC是弦,![]() ,
,![]() .
.
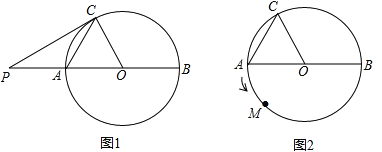
(1)在图1中,P为直径BA延长线上的一点,当CP与⊙O相切时,求PO的长;
(2)如图2,一动点M从A点出发,在⊙O上按逆时针方向运动一周,当![]() 时,求半径OM所扫过的扇形的面积.
时,求半径OM所扫过的扇形的面积.
【答案】(1)8;(2)![]() ;
;![]() ;
;![]() ;
;![]() .
.
【解析】
试题分析:(1)根据切线的性质得到CP⊥OC,由于∠OAC=∠AOC=60°,于是得到∠P=90°-∠AOC=30°,在Rt△POC中,求得CO=![]() PO=4,即可得到结论;
PO=4,即可得到结论;
(2)如图,当S△MAO=S△CAO时,动点M的位置有四种.①作点C关于直径AB的对称点M1,连接AM1,OM1,②过点M1作M1M2∥AB交⊙O于点M2,连接AM2,OM2,③过点C作CM3∥AB交⊙O于点M3,连接AM3,OM3,④当点M运动到C时,M与C重合,求得每种情况的OM转过的度数,再根据弧长公式求得弧AM的长,即可得到结论.
试题解析:(1)∵CP与⊙O相切,OC是半径.
∴CP⊥OC,
又∵∠OAC=∠AOC=60°,
∴∠P=90°-∠AOC=30°,
∴在Rt△POC中,CO=![]() PO=4,
PO=4,
则PO=2CO=8;
(2)如图,

①作点C关于直径AB的对称点M1,连接AM1,OM1.
易得S△M1AO=S△CAO,∠AOM1=60°∴当点M运动到M1时,S△MAO=S△CAO,
此时点M经过的弧长为![]() ,
,
∴半径OM所扫过的扇形的面积=![]() ;
;
②过点M1作M1M2∥AB交⊙O于点M2,连接AM2,OM2,易得S△M2AO=S△CAO.
∴∠AOM1=∠M1OM2=∠BOM2=60°
∴![]() 或
或![]() ,
,
∴当点M运动到M2时,S△MAO=S△CAO,此时点M经过的弧长为![]() ,
,
∴半径OM所扫过的扇形的面积=![]() ×
×![]() ×4=
×4=![]() π;
π;
③过点C作CM3∥AB交⊙O于点M3,连接AM3,OM3,易得S△M3AO=S△CAO
∴∠BOM3=60°,
∴![]() =
=![]() ×240或
×240或![]() =
=![]() ×2=
×2=![]()
∴当点M运动到M3时,S△MAO=S△CAO,此时点M经过的弧长为![]() ,
,
∴半径OM所扫过的扇形的面积=![]() ×
×![]() ×4=
×4=![]() ;
;
④当点M运动到C时,M与C重合,S△MAO=S△CAO,
此时点M经过的弧长为![]() ×300°或
×300°或![]() π+
π+![]() =
=![]()
∴半径OM所扫过的扇形的面积=![]() ×
×![]() ×4=
×4=![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某公司的拓展部有五个员工,他们每月的工资分别是3000元,4000元,5000元,7000元和10000元,那么他们工资的中位数是( )
A.4000元 B.5000元 C.7000元 D.10000元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,若将原图形上的每个点的横坐标都加上3,纵坐标保持不变,则所得图形的位置与原图形相比( )
A. 向上平移3个单位B. 向下平移3个单位C. 向右平移3个单位D. 向左平移3个单位
查看答案和解析>>
科目:初中数学 来源: 题型:
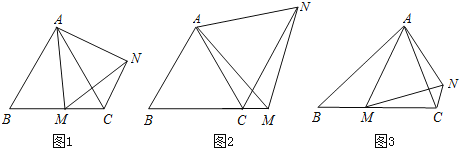
【题目】【提出问题】
(1)如图1,在等边△ABC中,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等边△AMN,连结CN.求证:∠ABC=∠ACN.
【类比探究】
(2)如图2,在等边△ABC中,点M是BC延长线上的任意一点(不含端点C),其它条件不变,(1)中结论∠ABC=∠ACN还成立吗?请说明理由.
【拓展延伸】
(3)如图3,在等腰△ABC中,BA=BC,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等腰△AMN,使顶角∠AMN=∠ABC.连结CN.试探究∠ABC与∠ACN的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以点D为中线把正方形ABCD的边DC顺时针旋转α度(0<α<360°)得DE,连接AE、BE.
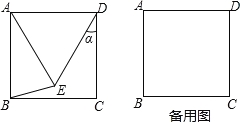
(1)当α=30时,求证:△ABE是等腰三角形;
(2)除30外,当α等于多少时,△ABE是等腰三角形?请直接写出α的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把抛物线y=-2x2+4x+1的图象向左平移2个单位,再向上平移3个单位,所得抛物线的函数关系式是( )
A.y=-2(x-1)2+6
B.y=-2(x-1)2—6
C.y=-2(x+1)2+6
D.y=-2(x+1)2—6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com