
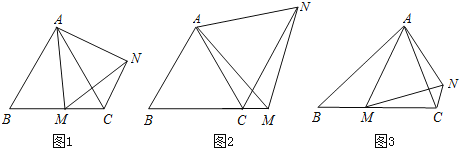
【题目】【提出问题】
(1)如图1,在等边△ABC中,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等边△AMN,连结CN.求证:∠ABC=∠ACN.
【类比探究】
(2)如图2,在等边△ABC中,点M是BC延长线上的任意一点(不含端点C),其它条件不变,(1)中结论∠ABC=∠ACN还成立吗?请说明理由.
【拓展延伸】
(3)如图3,在等腰△ABC中,BA=BC,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等腰△AMN,使顶角∠AMN=∠ABC.连结CN.试探究∠ABC与∠ACN的数量关系,并说明理由.
【答案】(1)见解析;(2)结论∠ABC=∠ACN仍成立;理由见解析;(3)∠ABC=∠ACN.
【解析】
试题分析:(1)利用SAS可证明△BAM≌△CAN,继而得出结论;
(2)也可以通过证明△BAM≌△CAN,得出结论,和(1)的思路完全一样.
(3)首先得出∠BAC=∠MAN,从而判定△ABC∽△AMN,得到![]() =
=![]() ,根据∠BAM=∠BAC﹣∠MAC,∠CAN=∠MAN﹣∠MAC,得到∠BAM=∠CAN,从而判定△BAM∽△CAN,得出结论.
,根据∠BAM=∠BAC﹣∠MAC,∠CAN=∠MAN﹣∠MAC,得到∠BAM=∠CAN,从而判定△BAM∽△CAN,得出结论.
(1)证明:∵△ABC、△AMN是等边三角形,
∴AB=AC,AM=AN,∠BAC=∠MAN=60°,
∴∠BAM=∠CAN,
∵在△BAM和△CAN中,
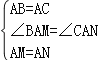
∴△BAM≌△CAN(SAS),
∴∠ABC=∠ACN.
(2)解:结论∠ABC=∠ACN仍成立;
理由如下:∵△ABC、△AMN是等边三角形,
∴AB=AC,AM=AN,∠BAC=∠MAN=60°,
∴∠BAM=∠CAN,
∵在△BAM和△CAN中,
∴△BAM≌△CAN(SAS),
∴∠ABC=∠ACN.
(3)解:∠ABC=∠ACN;
理由如下:∵BA=BC,MA=MN,顶角∠ABC=∠AMN,
∴底角∠BAC=∠MAN,
∴△ABC∽△AMN,
∴![]() =
=![]() ,
,
又∵∠BAM=∠BAC﹣∠MAC,∠CAN=∠MAN﹣∠MAC,
∴∠BAM=∠CAN,
∴△BAM∽△CAN,
∴∠ABC=∠ACN.


 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:初中数学 来源: 题型:
【题目】两名同学进行了10次三级蛙跳测试,经计算,他们的平均成绩相同,若要比较这两名同学的成绩哪一位更稳定,通常还需要比较他们成绩的( )
A.众数 B.中位数 C.方差 D.以上都不对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在⊙O中,AB为⊙O的直径,AC是弦,![]() ,
,![]() .
.
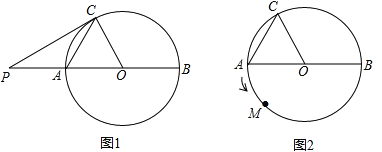
(1)在图1中,P为直径BA延长线上的一点,当CP与⊙O相切时,求PO的长;
(2)如图2,一动点M从A点出发,在⊙O上按逆时针方向运动一周,当![]() 时,求半径OM所扫过的扇形的面积.
时,求半径OM所扫过的扇形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2010年3月份,某市市区一周空气质量报告中某项污染指数的数据是:31,35,31,34,30,32,31,这组数据的中位数、众数分别是( )
A.32,31 B.31,32 C.31,31 D.32,35
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,点A的坐标为(0,1),点C的坐标为(4,3),回答下列问题(直接写出结果):
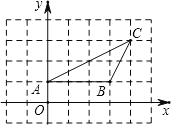
(1)点A关于原点对称的点的坐标为
(2)点C关于y轴对称的点的坐标为
(3)若△ABD与△ABC全等,则点D的坐标为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com