
【题目】如图,△ABC中,点A的坐标为(0,1),点C的坐标为(4,3),回答下列问题(直接写出结果):
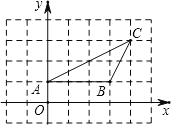
(1)点A关于原点对称的点的坐标为
(2)点C关于y轴对称的点的坐标为
(3)若△ABD与△ABC全等,则点D的坐标为 .
【答案】(1)、(0,-1),(2)、(-4,3),(3)、(4,-1)或(-1,3)或(-1,-1)或(4,3).
【解析】
试题分析:(1)、关于原点对称的点,横坐标与纵坐标都互为相反数; (2)、根据关于y轴对称的点,纵坐标相同,横坐标互为相反数,进行求解. (3)、因为△ABD与△ABC全等,则点D有两点,与点C关于直线AB对称和第二象限内的一点,从而得出答案.
试题解析:(1)∵点A的坐标为(0,1), ∴点A关于原点对称的点的坐标为(0,-1);
(2)∵点C的坐标为(4,3), ∴点C关于y轴对称的点的坐标为(-4,3),
(3)∵△ABD与△ABC全等, ∴点D的坐标为(4,-1)或(-1,3)或(-1,-1)或(4,3);


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,若将原图形上的每个点的横坐标都加上3,纵坐标保持不变,则所得图形的位置与原图形相比( )
A. 向上平移3个单位B. 向下平移3个单位C. 向右平移3个单位D. 向左平移3个单位
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【提出问题】
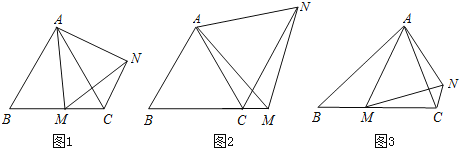
(1)如图1,在等边△ABC中,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等边△AMN,连结CN.求证:∠ABC=∠ACN.
【类比探究】
(2)如图2,在等边△ABC中,点M是BC延长线上的任意一点(不含端点C),其它条件不变,(1)中结论∠ABC=∠ACN还成立吗?请说明理由.
【拓展延伸】
(3)如图3,在等腰△ABC中,BA=BC,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等腰△AMN,使顶角∠AMN=∠ABC.连结CN.试探究∠ABC与∠ACN的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以点D为中线把正方形ABCD的边DC顺时针旋转α度(0<α<360°)得DE,连接AE、BE.
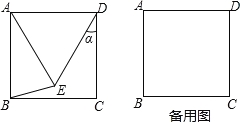
(1)当α=30时,求证:△ABE是等腰三角形;
(2)除30外,当α等于多少时,△ABE是等腰三角形?请直接写出α的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把抛物线y=-2x2+4x+1的图象向左平移2个单位,再向上平移3个单位,所得抛物线的函数关系式是( )
A.y=-2(x-1)2+6
B.y=-2(x-1)2—6
C.y=-2(x+1)2+6
D.y=-2(x+1)2—6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 图象的顶点横坐标是2,与
图象的顶点横坐标是2,与![]() 轴交于A(
轴交于A(![]() ,0)、B(
,0)、B(![]() ,0),
,0),![]() ﹤0﹤
﹤0﹤![]() ,与
,与![]() 轴交于点C,
轴交于点C,![]() 为坐标原点,
为坐标原点,![]() .
.
(1)求证:![]() ;
;
(2)求![]() 、
、![]() 的值;
的值;
(3)当![]() ﹥0且二次函数图象与直线
﹥0且二次函数图象与直线![]() 仅有一个交点时,求二次函数的最大值.
仅有一个交点时,求二次函数的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com