练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】命题“等角的补角相等”的题设_____________________，结论是_________________．

    【答案】 两个角是等角的补角 这两个角相等

    【解析】命题“等角的补角相等”的题设两个角是等角的补角，结论是这两个角相等．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】二次函数y=2x2﹣1的图象的顶点坐标是 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】a、b、c是直线，且a∥b，b⊥c，则a与c的位置关系是________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线y=ax2+bx+3与x轴相交于点A（﹣1，0）、B（3，0），与y轴相交于点C，点P为线段OB上的动点（不与O、B重合），过点P垂直于x轴的直线与抛物线及线段BC分别交于点E、F，点D在y轴正半轴上，OD=2，连接DE、OF．

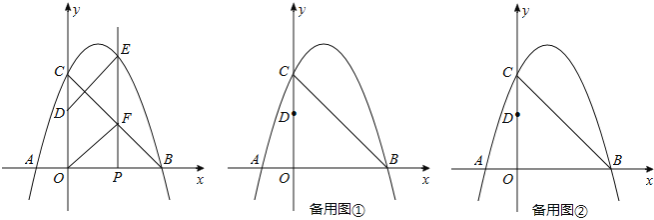
    （1）求抛物线的解析式；

    （2）当四边形ODEF是平行四边形时，求点P的坐标；

    （3）过点A的直线将（2）中的平行四边形ODEF分成面积相等的两部分，求这条直线的解析式．（不必说明平分平行四边形面积的理由）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某公司的拓展部有五个员工，他们每月的工资分别是3000元，4000元，5000元，7000元和10000元，那么他们工资的中位数是（ ）

    A．4000元 B．5000元 C．7000元 D．10000元

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列结论正确的是（ ）

    A. 0是正数也是有理数 B. 两数之积为正，这两数同为正

    C. 几个数相乘，积的符号由负因数的个数决定 D. 互为相反数的两个数的绝对值相等

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列数中：﹣8，2.7，0.66666…，0，2，9.181181118…是无理数的有（ ）

    A. 0个 B. 1个 C. 2个 D. 3个

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（1）化简：﹣3(x2+2xy)+6(x2﹣xy)

    （2）先化简，再求代数式的值：2(x2y+xy2)﹣2(x2y﹣2)﹣(xy2+2)，其中x=2016，y=﹣1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】【提出问题】

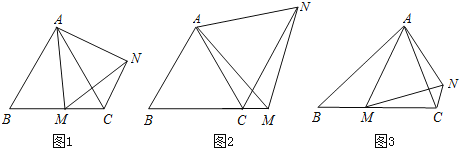
    （1）如图1，在等边△ABC中，点M是BC上的任意一点（不含端点B、C），连结AM，以AM为边作等边△AMN，连结CN．求证：∠ABC=∠ACN．

    【类比探究】

    （2）如图2，在等边△ABC中，点M是BC延长线上的任意一点（不含端点C），其它条件不变，（1）中结论∠ABC=∠ACN还成立吗？请说明理由．

    【拓展延伸】

    （3）如图3，在等腰△ABC中，BA=BC，点M是BC上的任意一点（不含端点B、C），连结AM，以AM为边作等腰△AMN，使顶角∠AMN=∠ABC．连结CN．试探究∠ABC与∠ACN的数量关系，并说明理由．

    查看答案和解析>>

    同步练习册答案