
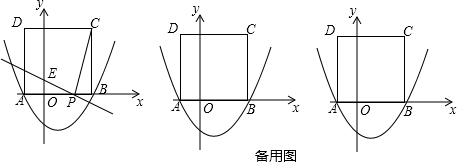
分析 (1)将点A的坐标代入二次函数的解析式求得其解析式,然后求得点B的坐标即可求得正方形ABCD的边长,从而求得点D的纵坐标;
(2)设PB=t,OE=l,利用△CBP∽△POE得到比例式,从而得到有关两个变量的二次函数,求最值即可;
(3)分点P位于y轴左侧和右侧两种情况讨论即可得到重叠部分的面积.
解答 解:(1)(-3,4);
将x=-1,y=0代入y=$\frac{1}{2}$x2-bx-$\frac{3}{2}$得:b=0,
∴函数解析式为y=$\frac{1}{2}$x2-x-$\frac{3}{2}$,
令y=0得:0=$\frac{1}{2}$x2-x-$\frac{3}{2}$,
解得:x1=3,x2=-1,
∴B(3,0)
∴AB═1+3=4,
∵ABCD是正方形,
∴BC=AB=4,
∴C(3,4);
(2)设PB=t,OE=l,则OP=3-t,
由∠CBP=∠POE=∠CPE=90°得△CBP∽△POE,
∴$\frac{4}{3-t}=\frac{t}{l}$,∴l=-$\frac{1}{4}$t2+$\frac{3}{4}$,
l=-$\frac{1}{4}(t-\frac{3}{2})^{2}+\frac{9}{16}$,
∴当t=$\frac{3}{2}$时,l有最大值$\frac{9}{16}$,
即P为BO中点时,OE的最大值为$\frac{9}{16}$;
(3)存在.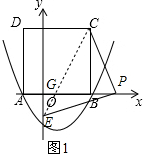
①点P点在y轴右侧时,CE交AB于点G,如图1,
在△PBC和△EOP中,
$\left\{\begin{array}{l}{∠CBP=∠POE}\\{PC=PE}\\{∠BCP=EPO}\end{array}\right.$,
∴△PBC≌△EOP(ASA),
∴OP=BC=4,
P点的坐标为(4,0),
∴PB=OP-BO=4-3=1,由△PBC≌△EOP得OE=PB=1
∵△BCG∽△OEG
∴BG:GO=BC:OE=4:1
∴BG=$\frac{4}{5}$BO=$\frac{12}{5}$,
∴重叠部分的面积=$\frac{1}{2}×4×\frac{12}{5}=\frac{24}{5}$,
②当P点在y轴左侧时,如图2,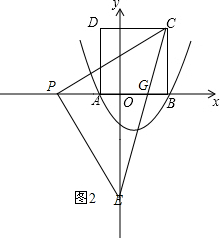
由△PBC≌△E0P可推出OP=BC=4,
P点的坐标为(-4,0),
此时重叠部分的面积为$\frac{712}{77}$.
点评 本题考查了正方形的性质、全等三角形的性质和判定、相似三角形的性质和判定、二次函数的综合知识、与二次函数的最值结合起来,主要考查学生的推理和计算能力,用了分类讨论思想.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:填空题
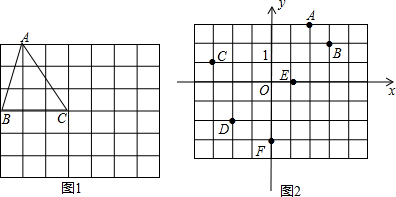
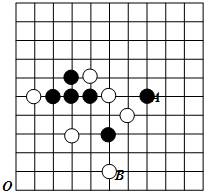 五子棋是一种两人对弈的棋类游戏,规则是:在正方形棋盘中,由黑方先行,白方后行,轮流弈子,下在棋盘横线与竖线的交叉点上,直到某一方首先在任一方向(横向、竖向或者是斜着的方向)上连成五子者为胜.如图,这一部分棋盘是两个五子棋爱好者的对弈图.观察棋盘,以点O为原点,在棋盘上建立平面直角坐标系,将每个棋子看成一个点,若黑子A的坐标为(7,5),则白子B的坐标为(5,1);为了不让白方获胜,此时黑方应该下在坐标为(3,7)或(7,3)的位置处.
五子棋是一种两人对弈的棋类游戏,规则是:在正方形棋盘中,由黑方先行,白方后行,轮流弈子,下在棋盘横线与竖线的交叉点上,直到某一方首先在任一方向(横向、竖向或者是斜着的方向)上连成五子者为胜.如图,这一部分棋盘是两个五子棋爱好者的对弈图.观察棋盘,以点O为原点,在棋盘上建立平面直角坐标系,将每个棋子看成一个点,若黑子A的坐标为(7,5),则白子B的坐标为(5,1);为了不让白方获胜,此时黑方应该下在坐标为(3,7)或(7,3)的位置处.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
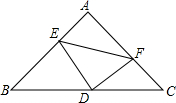 在等腰直角三角形中,AB=AC,点D是斜边BC的中点,点E、F分别为AB、AC边上的点,且DE⊥DF.
在等腰直角三角形中,AB=AC,点D是斜边BC的中点,点E、F分别为AB、AC边上的点,且DE⊥DF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com