Question

用黑白两种颜色的正六边形地面砖按如下所示的规律，拼成若干个图案．

（1）第5个图案中有白色地面砖______块；
（2）第n个图案中有白色地面砖______块．

Answer 1

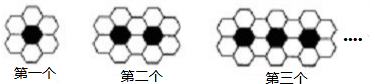
解：观察、分析图案，得到规律，第1个、第2个，第3个…个图案有白色地板砖分别是6，10，14…个，组成一个
公差是4，首项为6的等差数列．
因此（1）第5个图案中有白色地面砖有6+（5-1）×4=6+16=22
故答案为：22．
因此（2）第n个图案中有白色地面砖有6+（n-1）×4=6+4n-4=4n+2．
故答案为：4n+2．
分析：由图案发现规律，第1个图案有6个白色地面砖，第2个图案有6×2-2=10（个）白色地面砖
则第3个，第四个，…个图案有6×3-2×2=14，6×4-2×3=18，…（个）白色地面砖，
得到10，14，18，…公差是4的等差数列．
再由等差数列通项公式即可求出第5个图案和第n个图案中有白色地面砖有多少块．
点评：此题考查了学生观察、分析问题，总结归纳的能力．解题的关键是通过观察得到等差数列这个规律．