
已知:如图,四边形ABCD为平行四边形,以CD为直径作⊙O,⊙O与边BC相交于点F,⊙O的切线DE与边AB相交于点E,且AE=3EB.
(1)求证:△ADE∽△CDF;
(2)当CF:FB=1:2时,求⊙O与 ABCD的面积之比.
ABCD的面积之比.

(1)证明见解析;(2)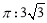 .
.
【解析】
试题分析:(1)根据平行四边形的性质得出∠A=∠C,AD∥BC,求出∠ADE=∠CDF,根据相似三角形的判定推出即可;
(2)设CF=x,FB=2x,则BC=3x,设EB=y,则AE=3y,AB=4y,根据相似得出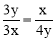 ,求出x=2y,由勾股定理得求出DF=
,求出x=2y,由勾股定理得求出DF=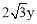 ,分别求出含参数y的⊙O面积和四边形ABCD面积,即可求出答案.
,分别求出含参数y的⊙O面积和四边形ABCD面积,即可求出答案.
试题解析:【解析】
(1)证明:∵CD是⊙O的直径,∴∠DFC=90°.
∵四边形ABCD是平行四边形,∴∠A=∠C,AD∥BC. ∴∠ADF=∠DFC=90°.
∵DE为⊙O的切线,∴DE⊥DC. ∴∠EDC=90°.
∴∠ADF=∠EDC=90°.∴∠ADE=∠CDF.
∵∠A=∠C,∴△ADE∽△CDE.
(2)∵CF:FB=1:2,∴设CF=x,FB=2x,则BC=3x.
∵AE=3EB,∴设EB=y,则AE=3y,AB=4y.
∵四边形ABCD是平行四边形,∴AD=BC=3x,AB=DC=4y.
∵△ADE∽△CDF,∴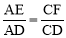 ,即
,即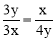 .
.
∵x、y均为正数,∴x=2y. ∴BC=6y,CF=2y.
在Rt△DFC中,∠DFC=90°,
由勾股定理得: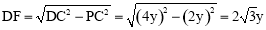 ,
,
∴⊙O的面积为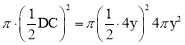 ,
,
四边形ABCD的面积为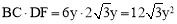 .
.
∴⊙O与四边形ABCD的面积之比为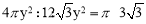 .
.
考点:1.圆周角定理;2. 平行四边形的性质;3.切线的性质;4.相似三角形的判定和性质;5.勾股定理;6.消参的待定系数法应用.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:初中数学 来源:2014年初中毕业升学考试(湖南岳阳卷)数学(解析版) 题型:填空题
观察下列一组数: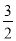 、1、
、1、 、
、 、
、 …,它们是按一定规律排列的那么这组数的第n个数是 .(n为正整数)
…,它们是按一定规律排列的那么这组数的第n个数是 .(n为正整数)
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(湖北武汉卷)数学(解析版) 题型:选择题
观察下列一组图形中的个数,其中第1个图中共有4个点,第2个图中共有10个点,第3个图中共有19个点,……,按此规律第5个图中共有点的个数是( )

A.31 B.46 C.51 D.66
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(湖北武汉卷)数学(解析版) 题型:选择题
若代数式 在实数范围内有意义,则x的取值范围是( )
在实数范围内有意义,则x的取值范围是( )
A.x≥-3 B.x>3 C.x≥3 D.x≤3
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(湖北宜昌卷)数学(解析版) 题型:选择题
如图,A,B两地被池塘隔开,小明通过下列方法测出了A、B间的距离:先在AB外选一点C,然后测出AC,BC的中点M,N,并测量出MN的长为12m,由此他就知道了A、B间的距离.有关他这次探究活动的描述错误的是( )

A. AB=24m B. MN∥AB
C. △CMN∽△CAB D. CM:MA=1:2
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(浙江舟山卷)数学(解析版) 题型:填空题
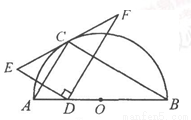
如图,点C在以AB为直径的半圆上,AB=8,∠CBA=30°,点D在线段AB上运动,点E与点D关于AC对称,DF⊥DE于点D,并交EC的延长线于点F.下列结论:①CE=CF;②线段EF的最小值为 ;③当AD=2时,EF与半圆相切;④若点F恰好落在BC上,则AD=
;③当AD=2时,EF与半圆相切;④若点F恰好落在BC上,则AD= ;⑤当点D从点A运动到点B时,线段EF扫过的面积是
;⑤当点D从点A运动到点B时,线段EF扫过的面积是 .其中正确结论的序号是 .
.其中正确结论的序号是 .
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(浙江温州卷)数学(解析版) 题型:解答题
八(1)班五位同学参加学校举办的数学竞赛,试卷中共有20道题,规定每题答对得5分,答错扣2分,未答得0分。赛后A,B, C,D,E五位同学对照评分标准回忆并记录了自己的答题情况(E同学只记得有7道题未答),具体如下表:
参赛同学 | 答对题数 | 答错题数 | 未答题数 |
A | 19 | 0 | 1 |
B | 17 | 2 | 1 |
C | 15 | 2 | 3 |
D | 17 | 1 | 2 |
E | / | / | 7 |
(1)根据以上信息,求A,B,C,D四位同学成绩的平均分;
(2)最后获知:A,B,C,D,E五位同学成绩分别是95分,81分,64分,83分,58分.
①求E同学的答对题数和答错题数;
②经计算,A,B,C,D四位同学实际成绩平均分是80.75分,与(1)中算得的平均分不相符,发现是其中一位同学记错了自己的答题情况.请指出哪位同学记错了,并写出他的实际答题情况(直接写出答案即可).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com