
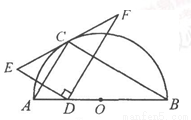
如图,点C在以AB为直径的半圆上,AB=8,∠CBA=30°,点D在线段AB上运动,点E与点D关于AC对称,DF⊥DE于点D,并交EC的延长线于点F.下列结论:①CE=CF;②线段EF的最小值为 ;③当AD=2时,EF与半圆相切;④若点F恰好落在BC上,则AD=
;③当AD=2时,EF与半圆相切;④若点F恰好落在BC上,则AD= ;⑤当点D从点A运动到点B时,线段EF扫过的面积是
;⑤当点D从点A运动到点B时,线段EF扫过的面积是 .其中正确结论的序号是 .
.其中正确结论的序号是 .
①③⑤.
【解析】
试题分析:①如图,连接CD,
∵根据轴对称的性质,CE=CD,∴∠DCE=∠ECD.
又∵DF⊥DE,∴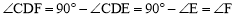 .∴CD=CF. ∴CE=CF. 结论①正确.
.∴CD=CF. ∴CE=CF. 结论①正确.

②∵由①知,EF=2CD,∴当线段EF最小时,线段CD也最小.
根据垂直线段最短的性质,当CD⊥AD时线段CD最小.
∵AB是半圆O 的直径,∴∠ACB=90°.
∵AB=8,∠CBA=30°,∴AC=4,BC=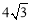 .
.
当CD⊥AD时,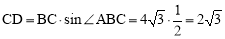 ,
,
∴线段EF的最小值为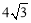 . 结论②错误.
. 结论②错误.
③如图,连接CD,CO,
∵∠CAB=90°,∠CBA=30°,∴∠CAB=60°. ∴△AOB是等边三角形,∴AO=4,∠OCA=60°.
∴当AD=2时,CD⊥AD,∠OCD=∠DOA=30°.
∵根据轴对称的性质,∠EOA=∠DOA=30°,∴∠ECO=90°.
∴EF与半圆相切. 结论③正确.

④若点F恰好落在BC上,则点D,F重合于点B,AD=AB=8. 结论④错误.
⑤当点D从点A运动到点B时,线段EF扫过的面积是△ABC面积的2倍,为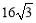 . 结论⑤正确.
. 结论⑤正确.
综上所述,结论正确的是①③⑤.
考点:1.单动点和轴对称问题;2. 轴对称的性质;3. 垂直线段的性质;4.圆周角定理;5.含30度角直角三角形的性质;6. 等边三角形的性质;7.切线的判定.


科目:初中数学 来源:2014年初中毕业升学考试(湖北宜昌卷)数学(解析版) 题型:解答题
已知:如图,四边形ABCD为平行四边形,以CD为直径作⊙O,⊙O与边BC相交于点F,⊙O的切线DE与边AB相交于点E,且AE=3EB.
(1)求证:△ADE∽△CDF;
(2)当CF:FB=1:2时,求⊙O与 ABCD的面积之比.
ABCD的面积之比.

查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(湖北宜昌卷)数学(解析版) 题型:选择题
作业时间是中小学教育质量综合评价指标的考查要点之一,腾飞学习小组五个同学每天课外作业时间分别是(单位:分钟):60,80,75,45,120.这组数据的中位数是( )
A. 45 B. 75 C. 80 D. 60
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(浙江舟山卷)数学(解析版) 题型:解答题
某汽车专卖店销售A,B两种型号的新能源汽车.上周售出1辆A型车和3辆B型车,销售额为96万元;本周已售2辆A型车和1辆B型车,销售额为62万元.
(1)求每辆A型车和B型车的售价各多少万元.
(2)甲公司拟向该店购买A,B两种型号的新能源汽车共6辆,购车费不少于130万元,且不超过140万元. 则有哪几种购车方案?
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(浙江舟山卷)数学(解析版) 题型:选择题
小红同学将自己5月份的各项消费情况制作成扇形统计图(如图),从图中可看出( )
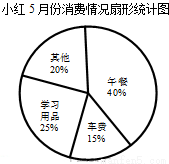
(A)各项消费金额占消费总金额的百分比
(B)各项消费的金额
(C)消费的总金额
(D)各项消费金额的增减变化情况
查看答案和解析>>
科目:初中数学 来源:2014年初中毕业升学考试(浙江杭州卷)数学(解析版) 题型:解答题
一个布袋中装有只有颜色不同的 个球,分别是2个白球,4个黑球,6个红球和b个黄球,从中任意摸出一个球,把摸出白球,黑球,红球的概率绘制成统计图(未绘制完整),请补全该统计图并求出
个球,分别是2个白球,4个黑球,6个红球和b个黄球,从中任意摸出一个球,把摸出白球,黑球,红球的概率绘制成统计图(未绘制完整),请补全该统计图并求出 的值.
的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com