
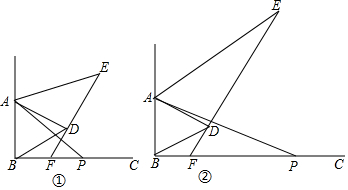
分析 (1)只要证明△PAB≌△EAD,可得∠ADE=∠ABP,由∠ABC=90°,推出∠ADE=90°,在四边形ABFD中,∠BFD=360°-∠BAD-∠ABF-∠ADF=120°,由此即可求出∠EFC.
(2)∠ADE与∠EFC的度数不发生变化.证明方法类似(1).
解答 解:(1)如图①中,
∵△ABD是等边三角形,
∴AB=AD,∠BAD=∠EAP=60°,
∴∠PAB=∠EAD,
在△PAB和△EAD中,
$\left\{\begin{array}{l}{PA=AE}\\{∠PAB=∠EAD}\\{AB=AD}\end{array}\right.$,
∴△PAB≌△EAD,
∴∠ADE=∠ABP,
∵∠ABC=90°,
∴∠ADE=90°,
在四边形ABFD中,∠BFD=360°-∠BAD-∠ABF-∠ADF=120°,
∴∠EFC=180°-∠BFD=60°.
(2)如图②中,∠ADE与∠EFC的度数不发生变化,理由如下,
∵△ABD是等边三角形,
∴AB=AD,∠BAD=∠EAP=60°,
∴∠PAB=∠EAD,
在△PAB和△EAD中,
$\left\{\begin{array}{l}{PA=AE}\\{∠PAB=∠EAD}\\{AB=AD}\end{array}\right.$,
∴△PAB≌△EAD,
∴∠ADE=∠ABP,
∵∠ABC=90°,
∴∠ADE=90°,
在四边形ABFD中,∠BFD=360°-∠BAD-∠ABF-∠ADF=120°,
∴∠EFC=180°-∠BFD=60°.
点评 本题考查全等三角形的判定和性质、等边三角形的性质、四边形内角和定理等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
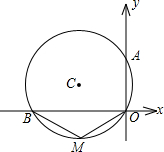 如图,⊙C过原点,且与两坐标轴分别交于点A、B,点A的坐标为(0,2),M为第三象限内弧$\widehat{OB}$上一点,∠BMO=120°,则⊙C的半径为2.
如图,⊙C过原点,且与两坐标轴分别交于点A、B,点A的坐标为(0,2),M为第三象限内弧$\widehat{OB}$上一点,∠BMO=120°,则⊙C的半径为2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
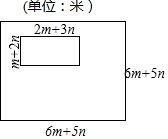 如图,某体育训练基地,有一块边长为(6m+5n)米的正方形土地,现准备在这块正方形土地上修建一个长为(2m+3n)米,宽为(m+2n)米的长方形游泳池,剩余部分则全部修建成休息区域.(结果化简)
如图,某体育训练基地,有一块边长为(6m+5n)米的正方形土地,现准备在这块正方形土地上修建一个长为(2m+3n)米,宽为(m+2n)米的长方形游泳池,剩余部分则全部修建成休息区域.(结果化简)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC中,AD是△ABC的边BC上的高,E、F分别是AB、AC的中点,AC=13、AB=20、BC=21.
如图,△ABC中,AD是△ABC的边BC上的高,E、F分别是AB、AC的中点,AC=13、AB=20、BC=21.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com