
【题目】如图,在ABCD中,E、F分别是AB、DC边上的点,且AE=CF, 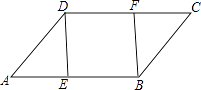
(1)求证:△ADE≌△CBF.
(2)若∠DEB=90°,求证:四边形DEBF是矩形.
【答案】
(1)证明:∵四边形ABCD是平行四边形,
∴AD=CB,∠A=∠C,
在△ADE和△CBF中,
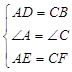 ,
,
∴△ADE≌△CBF(SAS)
(2)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∵AE=CF,
∴BE=DF,
∴四边形DEBF是平行四边形,
∵∠DEB=90°,
∴四边形DEBF是矩形
【解析】(1)由在ABCD中,AE=CF,可利用SAS判定△ADE≌△CBF.(2)由在ABCD中,且AE=CF,利用一组对边平行且相等的四边形是平行四边形,可证得四边形DEBF是平行四边形,又由∠DEB=90°,可证得四边形DEBF是矩形.
【考点精析】本题主要考查了平行四边形的性质和矩形的判定方法的相关知识点,需要掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分;有一个角是直角的平行四边形叫做矩形;有三个角是直角的四边形是矩形;两条对角线相等的平行四边形是矩形才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】随若移动终端设备的升级换代,手机已经成为我们生活中不可缺少的一部分,为了解中学生在假期使用手机的情况(选项:A .和同学亲友聊天;B.学习;C.购物;D.游戏;E.其它),端午节后某中学在全校范围内随机抽取了若干名学生进行调査,得到如下图表(部分信息未给出):

根据以上信息解答下列问题:
(1)这次被调查的学生有多少人?
(2)求表中![]() 的值,并补全条形统计图;
的值,并补全条形统计图;
(3)若该中学约有![]() 名学生,估计全校学生中利用手机购物或玩游戏的共有多少人?
名学生,估计全校学生中利用手机购物或玩游戏的共有多少人?
并根据以上调査结果,就中学生如何合理使用手机给出你的一条建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合:
(1)如图1,纸片ABCD中,AD=5,SABCD=15,过点A作AE⊥BC,垂足为E,沿AE剪下△ABE,将它平移至△DCE'的位置,拼成四边形AEE'D,则四边形AEE'D的形状为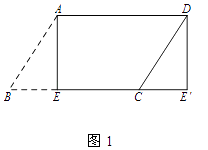
A.平行四边形
B.菱形
C.矩形
D.正方形
(2)如图2,在(1)中的四边形纸片AEE'D中,在EE'上取一点F,使EF=4,剪下△AEF,剪下△AEF,将它平移至△DE'F'的位置,拼成四边形AFF'D.
①求证:四边形AFF'D是菱形;
②求四边形AFF'D的两条对角线的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
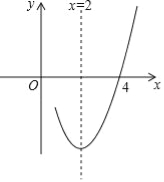
【题目】已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=2,与x轴的一个交点坐标为(4,0),其部分图象如图所示,下列结论:
①抛物线过原点;
②4a+b+c=0;
③a﹣b+c<0;
④抛物线的顶点坐标为(2,b);
⑤当x<2时,y随x增大而增大.
其中结论正确的是( )
A.①②③ B.③④⑤ C.①②④ D.①④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,真命题的个数是( )
①实数包括有理数、无理数和零;
②一个锐角加上一个钝角等于一平角;
③幂的乘方,底数不变,指数相加;
④平方根与立方根都等于它本身的数为1和0.
A. 3个 B. 2个 C. 1个 D. 0个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com