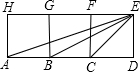
解：设正方形的边长是1，则AC=2，BC=1，CE=
，
∴
=
，
=
，
∴
=
，
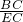
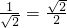
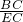
又∠BCE=∠ECA，
∴△ACE∽△ECB，
∴∠EAD=∠BEC，
∴∠EAD+∠EBD=∠BEC+∠EBD=∠ECD=45°．
分析：根据两条对应边的比相等，且夹角相等可以证明△ACE∽△ECB，再根据相似三角形的性质可以得到∠EAD=∠BEC，则∠EAD+∠EBD=∠BEC+∠EBD，再根据三角形的外角等于不相邻的两个内角的和，则所求的度数即为∠ECD的度数，根据正方形的性质即可求解．
点评：此题综合运用了相似三角形的判定以及性质、正方形的性质、勾股定理．
