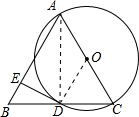
证明:连接AD,OD,如图所示:
∵OD=OC,
∴∠ODC=∠OCD,
∵DE为圆O的切线,
∴OD⊥DE,又DE⊥AB,
∴AB∥OD,
∴∠ODC=∠B,
∵AB=BC,
∴∠BAC=∠BCA,
∴∠BAC=∠BCA=∠B,
∴△ABC为等边三角形,
∴∠B=60°,
∵AC为直径,
∴AD⊥BC,又AB=AC,
∴BD=CD,
在Rt△BDE中,∠BDE=30°,
∴BD=2BE,
在Rt△BDA中,∠BAD=30°,
∴AB=2BD,
∴AB=4BE,
则AE=3BE.
分析:连接AD,OD,如图所示,由半径OD=OC,利用等边对等角得到一对角相等,由DE为圆O的切线,利用切线的性质得到OD⊥DE,再由DE⊥AB,利用垂直于同一条直线的两直线平行得到AB与OD平行,利用两直线平行同位角相等得到∠ODC=∠B,由AB=BC,利用等边对等角得到∠BAC=∠BCA,进而得到三角形ABC为等边三角形,得到∠BDE=∠BAD=30°,在直角三角形BDE中,利用30°所对的直角边等于斜边的一半得到BD=2BE,在直角三角形ABD中,同理得到AB=2BD,进而得到AB=4BE,即可得到AE=3BE,得证.
点评:此题考查了切线的性质,等边三角形的判定与性质,圆周角定理,以及含30°直角三角形的性质,熟练掌握性质及定理是解本题的关键.

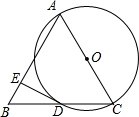 如图,在△ABC中,AB=BC,以AC为直径的⊙0与BC边交于点D,过点D作⊙O的切线DE,交AB于点E,若DE⊥AB.
如图,在△ABC中,AB=BC,以AC为直径的⊙0与BC边交于点D,过点D作⊙O的切线DE,交AB于点E,若DE⊥AB. 证明:连接AD,OD,如图所示:
证明:连接AD,OD,如图所示:

 阅读快车系列答案
阅读快车系列答案 如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为
如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为