
【题目】如图,在△ABC中,∠A=36°,AB=AC,AB的垂直平分线OD交AB于点O,交AC于点D,连接BD.下列结论错误的是( )

A. ∠C=2∠A B. BD平分∠ABC C. S△BCD=S△BOD D. 点D为线段AC的黄金分割点
科目:初中数学 来源: 题型:
【题目】全民健身和医疗保健是社会普遍关注的问题.2014年,某社区共投入30万元用于购买健身器材和药品.2015年,该社区购买健身器材的费用比上一年增加50%,购买药品的费用比上一年减少![]() ,但社区在这两方面的总投入仍与2014年相同.
,但社区在这两方面的总投入仍与2014年相同.
(1)求2014年社区购买药品的总费用;
(2)据统计,2014年该社区积极健身的家庭达到200户,但其药品费用明显减少,只占当年购买药品总费用的![]() .与2014年相比,如果2015年社区内健身家庭户数增加的百分数与平均每户健身家庭的药品费用降低的百分数相同,那么,2015年该社区用于健身家庭的药品费用就是当年购买健身器材费用的
.与2014年相比,如果2015年社区内健身家庭户数增加的百分数与平均每户健身家庭的药品费用降低的百分数相同,那么,2015年该社区用于健身家庭的药品费用就是当年购买健身器材费用的![]() .求2015年该社区健身家庭的户数.
.求2015年该社区健身家庭的户数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形纸片ABCD中,已知AD=8,AB=6,E是边BC上的点,以AE为折痕折叠纸片,使点B落在点F处,连接FC,当△EFC为直角三角形时,BE的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
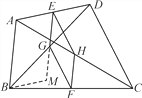
【题目】在四边形ABCD中,E、F分别是AD、BC的中点,G、H分别是BD、AC的中点,当AB、CD满足什么条件时,四边形EGFH是菱形?请证明你的结论.(提示:过点B作BM∥AD交EG的延长线于点M,证明EG//AB且EG=![]() AB)
AB)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2004年4月我国铁路第5次大提速。假设Kl20次空调快速列车的平均速度提速后比提速前提高了44千米/时,提速前的列车时刻表如下:
行驶区间 | 车次 | 起始时刻 | 到站时刻 | 历时 | 全程里程 |
A地—B地 | K120 | 2:00 | 6:00 | 4小时 | 264千米 |
请你根据题目提供的信息,填写提速后的列车时刻表,并写出计算过程。
行驶区间 | 车次 | 起始时刻 | 到站时刻 | 历时 | 全程里程 |
A地—B地 | K120 | 2:00 | 264千米 |
查看答案和解析>>
科目:初中数学 来源: 题型:
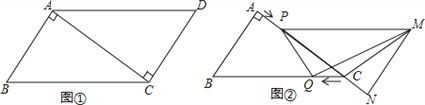
【题目】已知,如图①,在ABCD中,AB=3cm,BC=5cm,AC⊥AB,△ACD沿AC的方向匀速平移得到△PNM,速度为1cm/s;同时,点Q从点C出发,沿CB方向匀速移动,速度为1cm/s,当△PNM停止平移时,点Q也停止移动,如图②,设移动时间为t(s)(0<t<4),连接PQ,MQ,MC,解答下列问题:
(1)当t为何值时,PQ∥MN?
(2)设△QMC的面积为y(cm2),求y与t之间的函数关系式;
(3)是否存在某一时刻t,使S△QMC:S四边形ABQP=1:4?若存在,求出t的值;若不存在,请说明理由.
(4)是否存在某一时刻t,使PQ⊥MQ?若存在,求出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE、PF分别交AB、AC于点E、F,给出的以下四个结论:①AE=CF; ②△EPF一定是等腰直角三角形; ③S四边形AEPF=![]() S△ABC;④当∠EPF在△ABC内绕顶点P旋转时始终有EF=AP。(点E不与A、B重合),上述结论中始终正确的有_____.(写序号)
S△ABC;④当∠EPF在△ABC内绕顶点P旋转时始终有EF=AP。(点E不与A、B重合),上述结论中始终正确的有_____.(写序号)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com