
分析 (1)根据非负数的和为零,可得每个非负数同时为零,可得m,n的值;
(2)根据线段的和差,可得AP,PB的长,根据线段中点的性质,可得PQ的长,根据线段的和差,可得答案.
解答 解:(1)由(m-8)2+2|n-m+5|=0,得
m-8=0,n-m+5=0.
解得m=8,n=3;
(2)由(1)得AB=8,AP=3PB,
有两种情况:
①当点P在点B的左侧时,如图1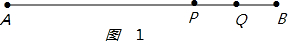 ,
,
AB=AP+PB=8,AP=3PB,
4PB=8,
解得PB=2,AP=3PB=3×2=6.
∵点Q为PB的中点,
∴PQ=$\frac{1}{2}$PB=1,
AQ=AP+PQ=6+1=7;
②当点P在点B的右侧时,如图2 ,
,
∵AP=AB+BP,AP=3PB,
∴3PB=8+PB,∴PB=4.
∵点Q为PB的中点,
∴BQ=$\frac{1}{2}$PB=2,
∴AQ=AB+BQ=8+2=10.
点评 本题考查了两点间的距离,利用非负数的和为零得出每个非负数同时为零是解题关键;利用线段的和差是解题关键,要分类讨论,以防遗漏.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
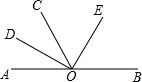 如图,AOB是一条直线,∠AOC=60°,OD,OE分别是∠AOC和∠BOC的平分线,则图中互补的角有( )
如图,AOB是一条直线,∠AOC=60°,OD,OE分别是∠AOC和∠BOC的平分线,则图中互补的角有( )| A. | 5对 | B. | 6对 | C. | 7对 | D. | 8对 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-5b)3=-15b3 | B. | (2x)3(-5xy2)=-40x4y2 | ||
| C. | 28x6y2+7x3y=4x2y | D. | (12a3-6a2+3a)÷3a=4a2-2a |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
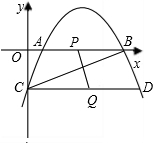 如图,抛物线y=-$\frac{1}{2}$x2+bx+c与x轴正半轴相交于点A(1,0)、B,与y轴相交于点C(0,-2).
如图,抛物线y=-$\frac{1}{2}$x2+bx+c与x轴正半轴相交于点A(1,0)、B,与y轴相交于点C(0,-2).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com