Question

20．如图，AB∥CD，点P是AB、CD之间的点，∠BAP=$\frac{1}{5}$∠BAC，∠PCD=$\frac{1}{5}$∠DCA，过点P作直线EF交AB，CD于点E，F，此时∠APE+∠CPF=（　　）

• A． 125°
• B． 135°
• C． 144°
• D． 154°

Answer 1

分析 先过P作PG∥AB，根据平行线的性质，即可得到∠BAP=∠APG，∠DCP=∠CPG，再根据AB∥CD，∠BAP=$\frac{1}{5}$∠BAC，∠PCD=$\frac{1}{5}$∠DCA，即可得出∠APG+∠CPG=∠APC=36°，进而得到结论．

解答 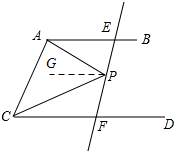解：如图所示，过P作PG∥AB，
∵AB∥CD，
∴PG∥CD，
∴∠BAP=∠APG，∠DCP=∠CPG，
∵AB∥CD，∠BAP=$\frac{1}{5}$∠BAC，∠PCD=$\frac{1}{5}$∠DCA，
∴∠BAP+∠PCD=$\frac{1}{5}$（∠BAC+∠DCA）=$\frac{1}{5}$×180°=36°，
即∠APG+∠CPG=∠APC=36°，
∴∠APE+∠CPF=180°-∠APC=180°-36°=144°，
故选：C．

点评 本题主要考查了平行线的性质的运用，解决问题的关键是作辅助线构造内错角，解题时注意：两直线平行，内错角相等．