

分析 (1)利用等量代换求出∠CAB=90°,用三角函数即可求出结论;
(2)先判断出四边形AODM为正方形,进而判断出△CMD≌△HOD,即可求出BH.
解答 解:(1)如图1,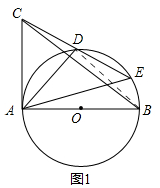 连接BD,
连接BD,
∵AB是⊙O的直径,
∴∠ADB=90°,
∴∠DAB+∠ABD=90°,
∵$\widehat{AD}=\widehat{AD}$,
∴∠CEA=∠ABD,
∵∠CAD=∠CEA,
∴∠CAD=∠ABD,
∴∠DAB+∠CAD=90°,
即∠CAB=90°,
∵$AC=2\sqrt{3}$,AB=6,
∴$tan∠ABC=\frac{AC}{AB}=\frac{{2\sqrt{3}}}{6}=\frac{{\sqrt{3}}}{3}$,
∴∠ABC=30°;
(2)
解:如图2,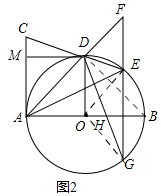 连接BD,OE,OG,
连接BD,OE,OG,
∵直径AB=6,
∴$OA=\frac{1}{2}AB=3$,
∵${\widehat{AD}}=\frac{3}{2}$π,
∴∠AOD=90°,
∵∠AOD=∠DMA=∠MAO=90°,OA=OD
∴四边形AODM为正方形,
∵OE=OG,EG⊥AB,
∴∠EOB=∠GOB,
∴∠EDB=∠GDB,
∵∠ADB=∠FDB=90°,
∴∠ADH=∠FDE=∠CDA,
∵∠ADM=∠ADO=45°,
∴∠CDM=∠HDO,
∵DM=DO,∠CMD=∠HOD=90°,
∴△CMD≌△HOD,
∴OH=CM=1,
∴BH=OB-OH=2.
点评 此题是圆的综合题,主要考查了等量代换,正方形的判定,全等三角形的判定,解(1)的关键是求出∠CAB=90°,解(2)的关键是判断出四边形AODM为正方形,是一道中等难度的中考常考题.


 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:初中数学 来源: 题型:选择题
| A. | 3$\sqrt{3}$×3$\sqrt{2}$=3$\sqrt{6}$ | B. | $\sqrt{27}$÷$\sqrt{3}$=3 | C. | 2$\sqrt{3}$+4$\sqrt{2}$=6$\sqrt{5}$ | D. | $\sqrt{(-7)^{2}}$=-7 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 二次函数y=ax2+bx+c(a≠0)的图象如图(虚线部分为对称轴),给出以下5个结论:①x≤1时,y随x的增大而增大;②abc>0;③b<a+c;④4a+2b+c>0;⑤3a-b<0,其中正确的结论有①④⑤(填上所有正确结论的序号).
二次函数y=ax2+bx+c(a≠0)的图象如图(虚线部分为对称轴),给出以下5个结论:①x≤1时,y随x的增大而增大;②abc>0;③b<a+c;④4a+2b+c>0;⑤3a-b<0,其中正确的结论有①④⑤(填上所有正确结论的序号).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,AB是⊙O的直径,点C是⊙O上一点,弧CF=弧CB,过点C作AB的垂线,垂足为D,连接BC、AC、BF,BF与C交于点E.
已知:如图,AB是⊙O的直径,点C是⊙O上一点,弧CF=弧CB,过点C作AB的垂线,垂足为D,连接BC、AC、BF,BF与C交于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在⊙O中,AB,BC为互相垂直且相等的两条弦,连接AC.求证:
如图,在⊙O中,AB,BC为互相垂直且相等的两条弦,连接AC.求证:查看答案和解析>>
科目:初中数学 来源: 题型:解答题

| 格点多边形各边上的 格点的个数 | 格点边多边形内部的 格点个数 | 格点多边形的面积 | |
| 多边形1 | 4 | 1 | 2 |
| 多边形2 | 5 | 2 | ②$\frac{7}{2}$ |
| 多边形3 | 6 | 3 | 5 |
| 多边形4 | ①5 | 4 | $\frac{11}{2}$ |
| 一般格点多边形 | m | n | S |

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com