
| 3 |
| 1×2×22 |
| 1 |
| 1×2 |
| 1 |
| 2×22 |
| 4 |
| 2×3×23 |
| 1 |
| 2×22 |
| 1 |
| 3×23 |
| 5 |
| 3×4×24 |
| 1 |
| 3×23 |
| 1 |
| 4×24 |
| 6 |
| 4×5×25 |
| 1 |
| 4×24 |
| 1 |
| 5×25 |
| n+2 |
| n(n+1)•2n+1 |
| 1 |
| n•2n |
| 1 |
| (n+1)•2n+1 |
| 1 |
| 1×2 |
| 1 |
| 2×22 |
| 1 |
| 2×22 |
| 1 |
| 3×23 |
| 1 |
| 3×23 |
| 1 |
| 4×24 |
| 1 |
| 4×24 |
| 1 |
| 5×25 |
| 1 |
| 20×220 |
| 1 |
| 21×221 |
| 1 |
| 2 |
| 1 |
| 21×221 |
| n+2 |
| n(n+1)•2n+1 |
| 1 |
| n•2n |
| 1 |
| (n+1)•2n+1 |
| 1 |
| 2 |
| 1 |
| 21×221 |


科目:初中数学 来源: 题型:
 如图,在南北方向的海岸线MN上,有A、B两艘巡逻船,现均收到故障船C的求救信号.已知A、B两船相距100(
如图,在南北方向的海岸线MN上,有A、B两艘巡逻船,现均收到故障船C的求救信号.已知A、B两船相距100(| 3 |
| 2 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 种植户 | 玫瑰花种植面积(亩) | 薰衣草种植面积(亩) | 卖花总收入(元) |
| 甲 | 5 | 3 | 33500 |
| 乙 | 3 | 7 | 43500 |
查看答案和解析>>
科目:初中数学 来源: 题型:
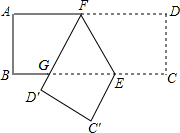 如图,已知在矩形ABCD中,点E在边BC上,BE=2CE,将矩形沿着过点E的直线翻折后,点C、D分别落在边BC下方的点C′、D′处,且点C′、D′、B在同一条直线上,折痕与边AD交于点F,D′F与BE交于点G.设AB=t,那么△EFG的周长为
如图,已知在矩形ABCD中,点E在边BC上,BE=2CE,将矩形沿着过点E的直线翻折后,点C、D分别落在边BC下方的点C′、D′处,且点C′、D′、B在同一条直线上,折痕与边AD交于点F,D′F与BE交于点G.设AB=t,那么△EFG的周长为查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com