
| 种植户 | 玫瑰花种植面积(亩) | 薰衣草种植面积(亩) | 卖花总收入(元) |
| 甲 | 5 | 3 | 33500 |
| 乙 | 3 | 7 | 43500 |
|
|
| 种植类型 | 种植面积(亩) | ||||
| 方案一 | 方案二 | 方案三 | 方案四 | 方案五 | |
| 玫瑰花 | 16 | 17 | 18 | 19 | 20 |
| 薰衣草 | 14 | 13 | 12 | 11 | 10 |


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
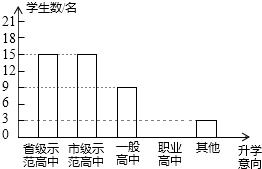 近几年我市加大中职教育投入力度,取得了良好的社会效果.某校随机调查了九年级m名学生的升学意向,并根据调查结果绘制出如下不完整的统计图表:
近几年我市加大中职教育投入力度,取得了良好的社会效果.某校随机调查了九年级m名学生的升学意向,并根据调查结果绘制出如下不完整的统计图表:| 升学意向 | 人数 | 百分比 |
| 省级示范高中 | 15 | 25% |
| 市级示范高中 | 15 | 25% |
| 一般高中 | 9 | n |
| 职业高中 | ||
| 其他 | 3 | 5% |
| 合计 | m | 100% |
查看答案和解析>>
科目:初中数学 来源: 题型:
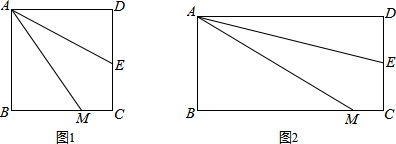
查看答案和解析>>
科目:初中数学 来源: 题型:
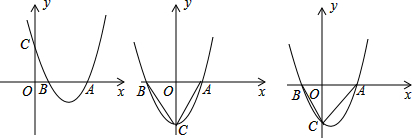
查看答案和解析>>
科目:初中数学 来源: 题型:
| • |
| 3 |
| • |
| 3 |
| 1 |
| 10 |
| 1 |
| 3 |
| • |
| 3 |
| 1 |
| 3 |
| •• |
| 45 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |
| 1×2×22 |
| 1 |
| 1×2 |
| 1 |
| 2×22 |
| 4 |
| 2×3×23 |
| 1 |
| 2×22 |
| 1 |
| 3×23 |
| 5 |
| 3×4×24 |
| 1 |
| 3×23 |
| 1 |
| 4×24 |
| 6 |
| 4×5×25 |
| 1 |
| 4×24 |
| 1 |
| 5×25 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com