
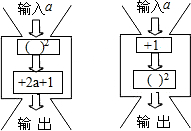
 分别给下面的两台数值转化机输入5个数据,比较它们的输出结果,你发观了什么规律?
分别给下面的两台数值转化机输入5个数据,比较它们的输出结果,你发观了什么规律?分析 任意取5个数据代入计算,可发现它们的输出结果相等;
(1)对于左边的数值转化机,先把a平方,再求它与2a+1的和;对于右边的数值转化机,先把a加1,然后求和的平方;
(2)利用计算的结果得到132.562+2×132.56×18.44+18.442=(132.56+18.44)2,然后计算151的平方即可.
解答 解:输入相同的数据,它们的输出结果相等;
(1)左边的数值转化机输出结果用a表示为a2+2a+1,右边的数值转化机输出结果用a表示为(a+1)2;
(2)由于a2+2a+1=(a+1)2,
所以132.562+2×132.56×18.44+18.442=(132.56+18.44)2=22801.
点评 本题考查了列代数式:把问题中与数量有关的词语,用含有数字、字母和运算符号的式子表示出来,就是列代数式.列代数式时,要先认真审题,抓住关键词语,仔细辩析词义,分清数量关系,列代数时要按要求规范地书写.也考查了代数式求值.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
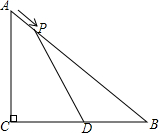 如图,在△ABC中,∠ACB=90°,AC=3cm,BC=4cm,点D为BC的中点.动点P从点A出发,沿着A→B方向以1cm/s的速度运动到点B停止运动.点P移动的时间为t秒,当△DBP为等腰三角形,求出t的值.
如图,在△ABC中,∠ACB=90°,AC=3cm,BC=4cm,点D为BC的中点.动点P从点A出发,沿着A→B方向以1cm/s的速度运动到点B停止运动.点P移动的时间为t秒,当△DBP为等腰三角形,求出t的值.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 月使用费 单位:元 | 主叫限制时间 单位:分 | 主叫超时费 单位:分 | 被叫 | |
| 方式一 | 30 | 150 | 0.25 | 免费 |
| 方式二 | 50 | 350 | 0.16 | 免费 |
| t≤150 | 150<t<350 | t=350 | t>350 | |
| 方式一 计费/元 | 30 | 0.25t-7.5 | 80 | 0.25t-7.5 |
| 方式二 计费/元 | 50 | 50 | 50 | 0.16t-6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
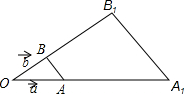 已知$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{0B}$=$\overrightarrow{b}$,$\overrightarrow{O{A}_{1}}$=3$\overrightarrow{a}$,$\overrightarrow{O{B}_{1}}$=3$\overrightarrow{b}$,试求$\overrightarrow{AB}$与$\overrightarrow{{A}_{1}{B}_{1}}$,并判断$\overrightarrow{AB}$与$\overrightarrow{{A}_{1}{B}_{1}}$是否共线(平行)?
已知$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{0B}$=$\overrightarrow{b}$,$\overrightarrow{O{A}_{1}}$=3$\overrightarrow{a}$,$\overrightarrow{O{B}_{1}}$=3$\overrightarrow{b}$,试求$\overrightarrow{AB}$与$\overrightarrow{{A}_{1}{B}_{1}}$,并判断$\overrightarrow{AB}$与$\overrightarrow{{A}_{1}{B}_{1}}$是否共线(平行)?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com