
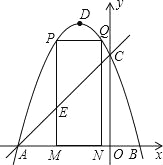
����Ŀ����ͼ��������y=��x2��2x+3 ��ͼ����x�ύ��A��B���㣨��A�ڵ�B����ߣ�����y�ύ�ڵ�C����DΪ�����ߵĶ��㣮
��1����A��B��C��������꣮
��2����MΪ�߶�AB��һ�㣨��M�����A��B�غϣ�������M��x��Ĵ��ߣ���ֱ��AC���ڵ�E���������߽��ڵ�P������P��PQ��AB���������ڵ�Q������Q��QN��x���ڵ�N������P�ڵ�Q��ߣ�������PMNQ���ܳ����ʱ������AEM�������
��3���ڣ�2���������£�������PMNQ���ܳ����ʱ������DQ������������һ��F��y���ƽ���ߣ���ֱ��AC���ڵ�G����G�ڵ�F���Ϸ�������FG=2DQ�����F�����꣮
���𰸡���1��A����3��0����B��1��0����C��0��3������2��![]() ����3��F����4����5����1��0����
����3��F����4����5����1��0����
��������
�����������1��ͨ������ʽ���ɵó�C�����꣬��y=0���ⷽ�̵ó����̵Ľ⣬�������A��B�����꣮
��2����M�������Ϊm����PM=��m2��2m+3��MN=����m��1����2=��2m��2������PMNQ���ܳ�=��2m2��8m+2������2m2��8m+2�䷽�����ݶ��κ��������ʣ����ɵó�m��ֵ��Ȼ�����ֱ��AC�Ľ���ʽ����x=m���������������εı߳����Ӷ���������ε������
��3����ȷ������D���꣬�����ó�FG��FG=4����������⼴�ɣ�
�����������1����������y=��x2��2x+3��֪��C��0��3����
��y=0����0=��x2��2x+3��
���x=��3��x=1��
����A����3��0����B��1��0����
��2����������y=��x2��2x+3=����x+1��2+4��֪���Գ���Ϊֱ��x=��1��
���M�ĺ�����Ϊm����PM=��m2��2m+3��MN=����m��1����2=��2m��2��
������PMNQ���ܳ�=2��PM+MN��=2����m2��2m+3��2m��2��=��2m2��8m+2=��2��m+2��2+10��
����m=��2ʱ���ε��ܳ����
����A����3��0����C��0��3����
��ֱ��AC�ĺ�������ʽΪy=x+3��
��x=��2ʱ��y=��2+3=1�����E����2��1����
��EM=1��AM=1��
��S=![]() AMEM=
AMEM=![]() ��
��
��3������M�ĺ�����Ϊ��2�������ߵĶԳ���Ϊx=��1��
����NӦ��ԭ���غϣ���Q���C�غϣ�
��DQ=DC��
��x=��1����y=��x2��2x+3����y=4��
����D����1��4����
��DQ=DC
��FG=2DQ��
��FG=4��
���F��n����n2��2n+3�������G��n��n+3����
����G�ڵ�F���Ϸ���
����n+3��������n2��2n+3��=4�����n=��4��n=1��
����F����4����5����1��0����


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס������ҿ���ͬʱ�뿪�ۿڣ����е��ٶȶ���40m/min��������15min�����A���ҿ�����20min�����B����A��B�����ֱ�߾���Ϊ1000m���������ű�ƫ��30���ķ����У����ҿ��ֵĺ��з�������ǣ�������
A. ��ƫ��30�� B. ��ƫ��30�� C. ��ƫ��60�� D. ��ƫ��60��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
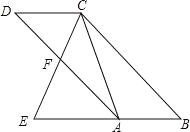
����Ŀ����ͼ����֪���ı���ABCD��ƽ���ı��Σ���E�ڱ�BA���ӳ����ϣ�CE��AD�ڵ�F����ECA=��D
��1����֤����EAC�ס�ECB��
��2����DF=AF����AC��BC��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������Ӱ���

���տ쵽�ˣ����Ҹ���������������ǹ�����ÿ�ұر������.С���İְָճа���һ����ʳ��.���룺һ��Ҫץס�̻�����������.Ϊ��������һ���Խ�.����Ѹ����ǹ������������Ӱ��ǣ������˿;Ϳ��Ի����ٵ�Ǯ�Ե����ֿ�ζ������.�������ѵ������е�6���ۼ�Ϊ11Ԫ/ǧ�˵����Ǻ�6���ۼ�Ϊ6Ԫ /ǧ�˵�ˮ���ǻ����һ�����100ǧ���ۼ�Ϊ8Ԫ/ǧ�˵��Ӱ��ǣ���ô��ȡ���ǡ�ˮ���Ǹ�����ǧ���أ�С���İְ����˰��죬Ҳû�н���������.���ϻؼҺ�ֻ����С����æ.û�뵽Ů�����������Ӿ��ҵ��˴�.
���װ�Ů���ķ�������Ӱ��ǣ���ʼ��������.�˿Ϳ����Ӱ���Ʒ����ȫ���۸�����Ը������.С����������.�ְָ��Ǹ��˵úϲ�£�죬����ֱ�������Ů��.��֪��С�����ְ߰����������Ӱ��ǵ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����и����߶�������������ε��ǣ�������
A. 2cm��3cm��5cm B. 5cm��6cm��10cm
C. 1cm��1cm��3cm D. 3cm��4cm��8cm
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
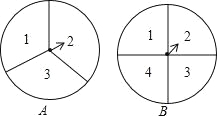
����Ŀ����ͼ��ת��A���������������ȣ��ֱ��������1��2��3��ת��B���ĸ����������ȣ��ֱ�������1��2��3��4��ת��A��Bת�̸�һ�Σ���ת��ֹͣת��ʱ����ָ�����������е�����������ˣ���ָ�������ĸ����εĽ�����ʱ������ת��ת�̣���
��1������״ͼ���б����г����п��ܳ��ֵĽ����
��2�����������ֵĻ�Ϊ�����ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���ACB=90�㣬D��BC�ӳ����ϵ�һ�㣬�߶�BD�Ĵ�ֱƽ����EG��AB�ڵ�E����BD�ڵ�G�� 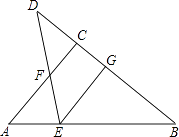
��1������B=30��ʱ��AE��EF��ʲô��ϵ����˵�����ɣ�
��2������D��BC�ӳ����ϣ�CD��BC���˶�ʱ����E�Ƿ����߶�AF�Ĵ�ֱƽ�����ϣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com