
【题目】阅读下列一段文字,然后回答下列问题.
已知在平面内两点P1(x1,y1)、P2(x2,y2),其两点间的距离![]() .例如P1(2,-4)、P2(7,8),其两点间的距离
.例如P1(2,-4)、P2(7,8),其两点间的距离![]() ,同时,当两点所在的直线再坐标轴或平行于坐标轴或垂直于坐标轴时,两点间距离公式可化简为|x2﹣x1|或|y2﹣y1|.
,同时,当两点所在的直线再坐标轴或平行于坐标轴或垂直于坐标轴时,两点间距离公式可化简为|x2﹣x1|或|y2﹣y1|.
(1)已知A(2,4)、B(-3,-8),试求A、B两点间的距离____.
(2)已知M、N在平行于y轴的直线上,点M的纵坐标为4,点N的纵坐标为-1,试求M、N 两点的距离为 .
(3)已知一个三角形各顶点坐标为D(1,6)、E(-2,2)、F(4,2),你能判定此三角形的形状吗?说明理由.
(4)在(3)的条件下,平面直角坐标中,在x轴上找一点P,使PD+PF的长度最短,求出点P的坐标及PD+PF的最短长度.
【答案】(1)13;(2)5;(3)△DEF为等腰三角形;(2)图详见解析,P(![]() ,0),PD+PF最短为
,0),PD+PF最短为![]() .
.
【解析】
(1)根据阅读材料中的A与B的坐标,利用两点间的距离公式求出A与B的距离即可;
(2)根据两点在平行于y轴的直线上,由M与N的纵坐标求出MN的距离即可;
(3)由三顶点坐标求出DE,DF,EF的长,即可判定此三角形形状;
(4)找出F关于x轴的对称点F′,连接DF′,与x轴交于P点,此时PD+PF最短,设直线DF′的解析式为y=kx+b,将D与F′的坐标代入求出k与b的值,确定出直线DF′解析式,令y=0求出x的值,确定出P坐标,由D与F′坐标,利用两点间的距离公式求出DF′的长,即为PD+PF的最短长度.
(1)∵A(2,4)、B(﹣3,﹣8),∴AB![]() 13;
13;
(2)∵M、N在平行于y轴的直线上,点M的纵坐标为4,点N的纵坐标为﹣1,∴MN=|4﹣(﹣1)|=5;
(3)△DEF为等腰三角形,理由为:
∵D(1,6)、E(﹣2,2)、F(4,2),∴DE![]() 5,DF
5,DF![]() 5,EF
5,EF![]() 6,即DE=DF,则△DEF为等腰三角形;
6,即DE=DF,则△DEF为等腰三角形;
(4)作F关于x轴的对称点F′,连接DF′,与x轴交于点P,此时DP+PF最短,设直线DF′解析式为y=kx+b,将D(1,6),F′(4,﹣2)代入得:![]() ,解得:
,解得: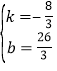 ,∴直线DF′解析式为y
,∴直线DF′解析式为y![]() ,令y=0,得:x
,令y=0,得:x![]() ,即P(
,即P(![]() ,0).
,0).
∵PF=PF′,∴PD+PF=DP+PF′=DF′![]() ,则PD+PF的长度最短时点P的坐标为(
,则PD+PF的长度最短时点P的坐标为(![]() ,0),此时PD+PF的最短长度为
,0),此时PD+PF的最短长度为![]() .
.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c与x轴交于点A(﹣1,0),顶点坐标为(1,n),与y轴的交点在(0,2)、(0,3)之间(包含端点).有下列结论:
①当x>3时,y<0;②3a+b>0;③﹣1≤a≤﹣ ![]() ;④
;④ ![]() ≤n≤4.
≤n≤4.
其中正确的是( )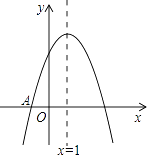
A.①②
B.③④
C.①③
D.①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步500m,先到终点
的人原地休息.已知甲先出发2s.在跑步过程中,甲、乙两人的距离y(m)与乙出发的时间t(s)之间的关系
如图所示,给出以下结论:①a=8;②b=92;③c=123.其中正确的是【 】

A.①②③ B.仅有①② C.仅有①③ D.仅有②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】重庆实验外国语学校每年四月初都定期举办体育文化节,初![]() 届周华同学为了在本次活动中获得更好的成绩,他让父亲带自己进行了体能训练,他们找了条笔直的跑道
届周华同学为了在本次活动中获得更好的成绩,他让父亲带自己进行了体能训练,他们找了条笔直的跑道![]() ,两人都从起点
,两人都从起点![]() 出发且一直保持匀速运动,父亲先出发两分钟后周华才出发,两人到达终点
出发且一直保持匀速运动,父亲先出发两分钟后周华才出发,两人到达终点![]() 后均停止运动,周华与父亲之间的距离
后均停止运动,周华与父亲之间的距离![]() (米)与周华出发的时间
(米)与周华出发的时间![]() (分)的关系如图所示,当周华到达终点时,父亲离终点的距离为________米.
(分)的关系如图所示,当周华到达终点时,父亲离终点的距离为________米.
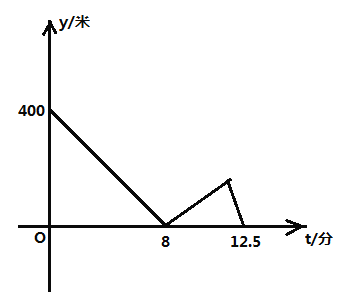
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人相约周末登花果山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,根据图象所提供的信息解答下列问题:
(1)甲登山上升的速度是每分钟 米,乙在A地时距地面的高度b为 米;
(2)若乙提速后,乙的登山上升速度是甲登山上升速度的3倍,请求出乙登山全程中,距地面的高度y(米)与登山时间x(分)之间的函数关系式;
(3)登山多长时间时,甲、乙两人距地面的高度差为70米?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A(0,1),M(3,2),N(4,4).动点P从点A出发,沿y轴以每秒1个单位长的速度向上移动,且过点P的直线l:y=﹣x+b也随之移动,设移动时间为t秒.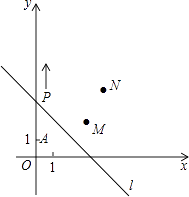
(1)当t=2时,则AP= , 此时点P的坐标是 .
(2)当t=3时,求过点P的直线l:y=﹣x+b的解析式?
(3)当直线l:y=﹣x+b从经过点M到点N时,求此时点P向上移动多少秒?
(4)点Q在x轴时,若S△ONQ=8时,请直按写出点Q的坐标是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对非负实数x“四舍五入”到个位的值记为(x).即当n为非负整数时,若![]() ,则(x)=n.如(0.46)=0,(3.67)=4.
,则(x)=n.如(0.46)=0,(3.67)=4.
给出下列关于(x)的结论:
①(1.493)=1;
②(2x)=2(x);
③若(![]() )=4,则实数x的取值范围是9≤x<11;
)=4,则实数x的取值范围是9≤x<11;
④当x≥0,m为非负整数时,有(m+2019x)=m+(2019x);
⑤(x+y)=(x)+(y);
其中,正确的结论有__________(填写所有正确的序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“一带一路”让中国和世界更紧密,“中欧铁路”为了安全起见在某段铁路两旁安置了两座可旋转探照灯.如图1所示,灯A射线从AM开始顺时针旋转至AN便立即回转,灯B射线从BP开始顺时针旋转至BQ便立即回转,两灯不停交叉照射巡视.若灯A转动的速度是每秒2度,灯B转动的速度是每秒1度.假定主道路是平行的,即PQ∥MN,且∠BAM:∠BAN=2:1.
(1)填空:∠BAN=_____°;
(2)若灯B射线先转动30秒,灯A射线才开始转动,在灯B射线到达BQ之前,A灯转动几秒,两灯的光束互相平行?
(3)如图2,若两灯同时转动,在灯A射线到达AN之前.若射出的光束交于点C,过C作∠ACD交PQ于点D,且∠ACD=120°,则在转动过程中,请探究∠BAC与∠BCD的数量关系是否发生变化?若不变,请求出其数量关系;若改变,请说明理由.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,E、F、G、H依次是各边中点,O是形内一点,若四边形AEOH、四边形BFOE、四边形CGOF的面积分别是4、5、6,则四边形DHOG的面积是( )
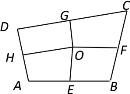
A. 5B. 4C. 8D. 6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com