
如图,在△ABC中,∠C=90º,AC=6cm,BC=8cm,D、E分别是AC、AB
的中点,连接DE.点P从点D出发,沿DE方向匀速运动,速度为1cm/s;同时,点Q从点B出发,沿
BA方向匀速运动,速度为2cm/s,当点P停止运动时,点Q也停止运动.连接PQ,设运动时间为t(0<t
<4)s.解答下列问题:
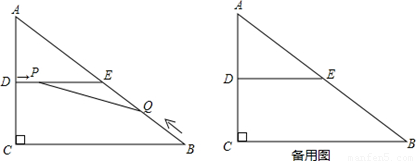
(1)当t为何值时,PQ⊥AB?
(2)当点Q在B、E之间运动时,设五边形PQBCD的面积为ycm2,求y与t之间的函数关系式;
(3)在(2)的情况下,是否存在某一时刻t,使得PQ分四边形BCDE所成的两部分的面积之比为
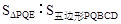 =1∶29?若存在,求出此时t的值以及点E到PQ的距离h;若不存在,请说明理由.
=1∶29?若存在,求出此时t的值以及点E到PQ的距离h;若不存在,请说明理由.
(1)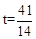 (2)y
(2)y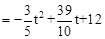 (3)当
(3)当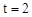 时,h
时,h
【解析】解:(1)如图,
在Rt△ABC中,AC=6,BC=8,
∴ 。
。
∵点D、E分别是AC、AB的中点,
∴AD=DC=3,AE=EB=5,DE∥BC,且DE=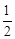 BC=4。
BC=4。
∵PQ⊥AB,∴∠PQB=∠C=900。
又∵DE∥BC,∴∠AED=∠B。
∴△PQE∽△ABC。∴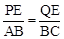 。
。
由题意,得PE=4-t,QE=2t-5,
∴ ,解得
,解得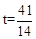 。
。
∴当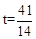 时,PQ⊥AB。
时,PQ⊥AB。
(2)过点P作PM⊥AB于点M。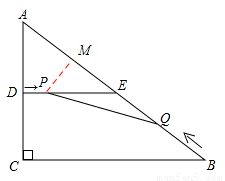
由△PME∽△ABC,得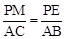 ,
,
∴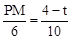 ,即
,即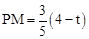 。
。
∴ ,
,
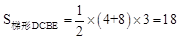 。
。
∴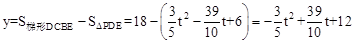 。
。
(3)假设存在时刻t使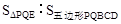 =1∶29,此时,
=1∶29,此时,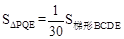 ,
,
∴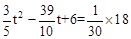 ,即
,即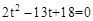 。
。
解得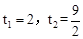 (舍去)。
(舍去)。
当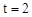 时,PM=
时,PM=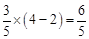 ,ME=
,ME=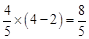 ,EQ=5-2×2=1,
,EQ=5-2×2=1,
MQ=ME+EQ=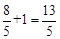 ,
,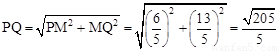 。
。
∵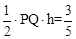 ,∴
,∴ 。
。
当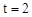 时, PQ分四边形BCDE所成的两部分的面积之比为
时, PQ分四边形BCDE所成的两部分的面积之比为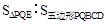 =1∶29,此时点E到PQ的距离h
=1∶29,此时点E到PQ的距离h 。
。
(1)由△PQE∽△ABC可列式求解。
(2)由△PME∽△ABC可求得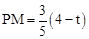 ,根据
,根据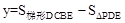 可求关系式。
可求关系式。
(3)假设存在,由已知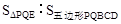 =1∶29可得
=1∶29可得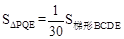 ,即可求出
,即可求出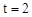 ,进一步由
,进一步由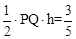 求出
求出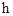 。
。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
 如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为
如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为A、
| ||||
B、(
| ||||
C、
| ||||
D、
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com