

分析 (1)根据扇形统计图即可解决问题.
(2)根据条形统计图,可知2013你那该市市区空气质量为良好的天数为211天,占全年的百分比约为$\frac{211}{365}$×100%.
(3)2013年该市市区空气质量为重度污染的天数为365×(1-66.7%-20%).
解答 解:(1)根据扇形统计图可知2013年该市市区空气质量为中度污染的天数占全年空气污染天数的百分比是20%.
故答案为20%.
(2)由条形统计图可知2013你那该市市区空气质量为良好的天数为211天,占全年的百分比约为$\frac{211}{365}$×100%≈57.8%,
故答案为211,57.8%.
(3)2013年该市市区空气质量为重度污染的天数为365×(1-66.7%-20%)≈49天.
点评 本题考查条形统计图、扇形统计图等知识,解题的关键是灵活运用所学知识解决问题,属于基础题,中考常考题型.


科目:初中数学 来源: 题型:解答题
 2016无锡“五一”车展期间,某公司对参观车展的且有购车意向的消费者进行了随机问卷调查,共发放900份调查问卷,并收回有效问卷750份.工作人员对有效调查问卷作了统计,其中,将消费者年收入的情况整理后,制成表格如下:
2016无锡“五一”车展期间,某公司对参观车展的且有购车意向的消费者进行了随机问卷调查,共发放900份调查问卷,并收回有效问卷750份.工作人员对有效调查问卷作了统计,其中,将消费者年收入的情况整理后,制成表格如下:| 年收入(万元) | 4.8 | 6 | 7.2 | 9 | 10 |
| 被调查的消费者人数(人) | 150 | 338 | 160 | 60 | 42 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
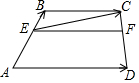 如图,在梯形ABCD中,AD∥BC,AD=3,BC=2,点E、F分别在两腰上,
如图,在梯形ABCD中,AD∥BC,AD=3,BC=2,点E、F分别在两腰上,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中.直线y=-x+3与x轴交于点B,与y轴交于点C,抛物线y=ax2+bx+c经过B,C两点,与x轴负半轴交于点A,连结AC,tan∠CAB=3
如图,在平面直角坐标系中.直线y=-x+3与x轴交于点B,与y轴交于点C,抛物线y=ax2+bx+c经过B,C两点,与x轴负半轴交于点A,连结AC,tan∠CAB=3查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,在△ABC中,∠ABC=45°,AD是BC边上的中线,过点D作DE⊥AB于点E,且sin∠DAB=$\frac{3}{5}$,DB=3$\sqrt{2}$.求:
已知:如图,在△ABC中,∠ABC=45°,AD是BC边上的中线,过点D作DE⊥AB于点E,且sin∠DAB=$\frac{3}{5}$,DB=3$\sqrt{2}$.求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com