
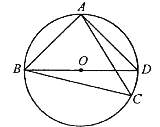
【题目】如图,![]() 为
为![]() 的外接圆上的一动点(点
的外接圆上的一动点(点![]() 不在
不在![]() 上,且不与点
上,且不与点![]() 、
、![]() 重合),
重合),![]() .
.
(1)求证:![]() 是该外接圆的直径;
是该外接圆的直径;
(2)连接![]() ,求证:涯
,求证:涯![]() ;
;
(3)若![]() 关于直线
关于直线![]() 的对称图形为
的对称图形为![]() ,连接
,连接![]() ,试探究
,试探究![]() 、
、![]() 、
、![]() 三者之间满足的等量关系,并证明你的结论.
三者之间满足的等量关系,并证明你的结论.
【答案】见解析
【解析】试题分析:(1)要证明BD是该外接圆的直径,只需要证明∠BAD是直角即可,又因为∠ABD=45°,所以需要证明∠ADB=45°;
(2)在CD延长线上截取DE=BC,连接EA,只需要证明△EAF是等腰直角三角形即可得出结论;
(3)过点M作MF⊥MB于点M,过点A作AF⊥MA于点A,MF与AF交于点F,证明△AMF是等腰三角形后,可得出AM=AF,MF=![]() AM,然后再证明△ABF≌△ADM可得出BF=DM,最后根据勾股定理即可得出DM2,AM2,BM2三者之间的数量关系.
AM,然后再证明△ABF≌△ADM可得出BF=DM,最后根据勾股定理即可得出DM2,AM2,BM2三者之间的数量关系.
解: (1) (1)∵![]() ,
,
∴∠ACB=∠ADB=45°,
∵∠ABD=45°,
∴∠BAD=90°,
∴BD是△ABD外接圆的直径;
(2)在![]() 的延长线上截取
的延长线上截取![]() ,连接
,连接![]()
因为![]()
所以![]()
因为![]() ,
,![]()
所以![]()
在![]() 与
与![]() 中,
中,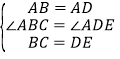
所以![]()
所以![]()
所以![]()
即![]()
因为![]()
所以![]()
所以![]() 是等腰直角三角形
是等腰直角三角形
所以![]()
所以![]()
(3)过点![]() 作
作![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,连接
,连接![]()
由对称性可知![]()
所以![]()
所以![]() 是等腰直角三角形
是等腰直角三角形
所以![]()
因为![]()
所以![]()
在![]() 与
与![]() 中,
中,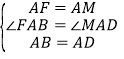
所以![]()
所以![]()
在![]() 中,因为
中,因为![]()
所以![]()


科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程x2﹣(m﹣3)x﹣m2=0.
(1)证明:方程总有两个不相等的实数根;
(2)设这个方程的两个实数根为x1,x2,且|x1|=|x2|﹣2,求m的值及方程的根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形网格中每个小正方形边长都是1.
(1)画出△ABC关于直线1对称的图形△A1BlCl;
(2)在直线l上找一点P,使PB=PC;(要求在直线1上标出点P的位置)
(3)连接PA、PC,计算四边形PABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°,∠ABC=30°,AC=2,△ABC绕点C顺时针旋转得△A1B1C,当A1落在AB边上时,连接B1B,取BB1的中点D,连接A1D,则A1D的长度是 ( )

A. ![]() B. 2
B. 2![]() C. 3 D. 2
C. 3 D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平行四边形ABCD中,E,F是对角线BD上的两点, 如果添加一个条件使△ABE≌△CDF,则添加的条件不能是( )

A. AE=CF B. BE=FD C. BF=DE D. ∠1=∠2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每年的6月5日为世界环保日,为了提倡低碳环保,某公司决定购买10台节省能源的新设备,现有甲乙两种型号的设备可供选购.经调查:购买3台甲型设备比购买2台乙型设备多花14万元,购买2台甲型设备比购买3台乙型设备少花4万元.
(1)直接写出甲乙两种型号设备每台的价格分别为多少万元;
(2)该公司经预算决定购买节省能源的新设备的资金不超过90万元,你认为该公司有几种购买方案?
(3)在(2)的条件下,若该公司使用新设备进行生产,已知甲型设备每台的产量为240吨/月,乙型设备每台的产量为180吨/月,每月要求总产量不低于2040吨,请你为该公司设计一种最省钱的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 的中点,
的中点,![]() ,垂足为
,垂足为![]() ,连接
,连接![]() .
.

(1)如图1,![]() 与
与![]() 的数量关系是__________.
的数量关系是__________.
(2)如图2,若![]() 是线段
是线段![]() 上一动点(点
上一动点(点![]() 不与点
不与点![]() 、
、![]() 重合),连接
重合),连接![]() ,将线段
,将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到线段
得到线段![]() ,连接
,连接![]() ,请猜想
,请猜想![]() 三者之间的数量关系,并证明你的结论;
三者之间的数量关系,并证明你的结论;
查看答案和解析>>
科目:初中数学 来源: 题型:
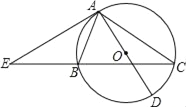
【题目】如图,△ABC内接于⊙O,AD是⊙O直径,过点A的切线与CB的延长线交于点E.
(1)求证:EA2=EBEC;
(2)若EA=AC,cos∠EAB=![]() ,AE=12,求⊙O的半径.
,AE=12,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小亮想了解一根弹簧的长度是如何随所挂物体质量的变化而变化的,他把这根弹簧的上端固定,在其下端悬挂物体.下面是小亮测得的弹簧的长度y与所挂物体质量x的几组对应值.
所挂质量x/kg | 0 | 1 | 2 | 3 | 4 | 5 |
弹簧长度y/cm | 30 | 32 | 34 | 36 | 38 | 40 |
(1)上表所反映的变化过程中的两个变量,________是自变量,________是因变量;
(2)直接写y与x的关系式;
(3)当弹簧长度为130cm(在弹簧承受范围内)时,求所挂重物的质量.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com