
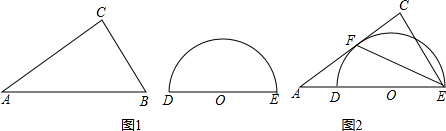
分析 (1)由当点B于点O重合的时候,BO=OD+BD=4cm,又由三角板以2cm/s的速度向右移动,即可求得三角板运动的时间;
(2)①连接OF,由AC与半圆相切于点F,易得OF⊥AC,然后由∠ACB=90°,易得OF∥CE,继而证得EF平分∠AEC;
②由△AFO是直角三角形,∠BAC=30°,OF=OD=3cm,可求得AF的长,由EF平分∠AEC,易证得△AFE是等腰三角形,且AF=EF,则可求得答案.
解答 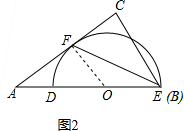 解:(1)∵当点B于点O重合的时候,BO=OD+BD=4cm,
解:(1)∵当点B于点O重合的时候,BO=OD+BD=4cm,
∴t=$\frac{4}{2}$=2(s);
∴三角板运动的时间为:2s;
(2)①证明:连接O与切点F,则OF⊥AC,
∵∠ACE=90°,
∴EC⊥AC,
∴OF∥CE,
∴∠OFE=∠CEF,
∵OF=OE,
∴∠OFE=∠OEF,
∴∠OEF=∠CEF,
即EF平分∠AEC;
②解:由①知:OF⊥AC,
∴△AFO是直角三角形,
∵∠BAC=30°,OF=OD=3cm,
∴tan30°=$\frac{3}{AF}$,
∴AF=3$\sqrt{3}$cm,
由①知:EF平分∠AEC,
∴∠AEF=∠CEF=$\frac{1}{2}$∠AEC=30°,
∴∠AEF=∠EAF,
∴△AFE是等腰三角形,且AF=EF,
∴EF=3$\sqrt{3}$cm.
点评 此题属于圆的综合题.考查了切线的性质、等腰三角形的判定与性质以及三角函数等知识.注意准确作出辅助线是解此题的关键.


 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
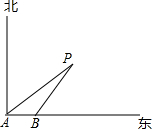 如图,一艘轮船以18海里/时的速度由西向东方向航行,行至A处测得灯塔P在它的北偏东60°的方向上,继续向东行驶20分钟后,到达B处又测得灯塔P在它的北偏东45°方向上,求轮船与灯塔的最短距离.(精确到0.1,$\sqrt{3}$≈1.73)
如图,一艘轮船以18海里/时的速度由西向东方向航行,行至A处测得灯塔P在它的北偏东60°的方向上,继续向东行驶20分钟后,到达B处又测得灯塔P在它的北偏东45°方向上,求轮船与灯塔的最短距离.(精确到0.1,$\sqrt{3}$≈1.73)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3.284×108 | B. | 32.84×107 | C. | 3.284×107 | D. | 32.84×108 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com