
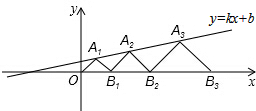
 如图,在平面直角坐标系xOy中,点A1,A2,A3,…和B1,B2,B3,…分别在直线y=kx+b和x轴上,△OA1B1,△B1A2B2,△B2A3B3,…都是等腰直角三角形,如果A1(1,1),A2($\frac{7}{2}$,$\frac{3}{2}$),那么点A3的纵坐标是$\frac{9}{4}$,点An的纵坐标是($\frac{3}{2}$)n-1.
如图,在平面直角坐标系xOy中,点A1,A2,A3,…和B1,B2,B3,…分别在直线y=kx+b和x轴上,△OA1B1,△B1A2B2,△B2A3B3,…都是等腰直角三角形,如果A1(1,1),A2($\frac{7}{2}$,$\frac{3}{2}$),那么点A3的纵坐标是$\frac{9}{4}$,点An的纵坐标是($\frac{3}{2}$)n-1. 分析 先求出直线y=kx+b的解析式,求出直线与x轴、y轴的交点坐标,求出直线与x轴的夹角的正切值,分别过等腰直角三角形的直角顶点向x轴作垂线,然后根据等腰直角三角形斜边上的高线与中线重合并且等于斜边的一半,利用正切值列式依次求出三角形的斜边上的高线,即可得到A3的坐标,进而得出各点的坐标的规律.
解答 解:∵A1(1,1),A2($\frac{7}{2}$,$\frac{3}{2}$)在直线y=kx+b上,
∴$\left\{\begin{array}{l}{k+b=1}\\{\frac{7}{2}k+b=\frac{3}{2}}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=\frac{1}{5}}\\{b=\frac{4}{5}}\end{array}\right.$,
∴直线解析式为:y=$\frac{1}{5}$x+$\frac{4}{5}$;
设直线与x轴、y轴的交点坐标分别为N、M,
当x=0时,y=$\frac{4}{5}$,
当y=0时,$\frac{1}{5}$x+$\frac{4}{5}$=0,
解得x=-4,
∴点M、N的坐标分别为M(0,$\frac{4}{5}$),N(-4,0),
∴tan∠MNO=$\frac{MO}{NO}$=$\frac{\frac{4}{5}}{4}$=$\frac{1}{5}$,
作A1C1⊥x轴与点C1,A2C2⊥x轴与点C2,A3C3⊥x轴与点C3,
∵A1(1,1),A2($\frac{7}{2}$,$\frac{3}{2}$),
∴OB2=OB1+B1B2=2×1+2×$\frac{3}{2}$=2+3=5,
tan∠MNO=$\frac{{A}_{3}{C}_{3}}{N{C}_{3}}$=$\frac{{A}_{3}{C}_{3}}{4+5+{B}_{3}{C}_{3}}$=$\frac{1}{5}$,
∵△B2A3B3是等腰直角三角形,
∴A3C3=B2C3,
∴A3C3=$\frac{9}{4}$=($\frac{3}{2}$)2,
同理可求,第四个等腰直角三角形A4C4=$\frac{27}{8}$=($\frac{3}{2}$)3,
依此类推,点An的纵坐标是($\frac{3}{2}$)n-1,
故答案为:$\frac{9}{4}$,($\frac{3}{2}$)n-1.
点评 本题考查的是一次函数图象上点的坐标特点,熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:选择题
 如图,这是2016年12月的日历表,任意圈出一竖列上相邻的四个数,请你运用方程的思想来研究,发现这四个数的和不可能是( )
如图,这是2016年12月的日历表,任意圈出一竖列上相邻的四个数,请你运用方程的思想来研究,发现这四个数的和不可能是( )| A. | 50 | B. | 58 | C. | 68 | D. | 70 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.612×107 | B. | 6.12×106 | C. | 61.2×105 | D. | 612×106 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a=-2,b=-3 | B. | a=2,b=3 | C. | a=-2,b=3 | D. | a=2,b=-3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com