
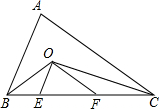
 如图,△ABC中,BC=10cm,BO与CO分别为∠ABC与∠ACB的平分线,OE∥AB,OF∥AC,求△OEF的周长.
如图,△ABC中,BC=10cm,BO与CO分别为∠ABC与∠ACB的平分线,OE∥AB,OF∥AC,求△OEF的周长. 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案科目:初中数学 来源: 题型:
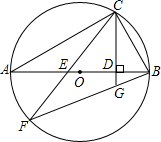 如图,已知AB是⊙O的直径,点C是⊙O上一点,连接BC,过点C作直线CD⊥AB于点D,弦CF与AB交于点E,弦BF与直线CD交于点G.已知BG=2,GF=4,求:BC的长度.
如图,已知AB是⊙O的直径,点C是⊙O上一点,连接BC,过点C作直线CD⊥AB于点D,弦CF与AB交于点E,弦BF与直线CD交于点G.已知BG=2,GF=4,求:BC的长度.查看答案和解析>>
科目:初中数学 来源: 题型:
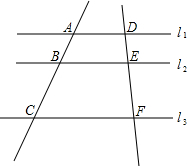 已知:如图,l1∥l2∥l3,则在下列比例中一定成立的是( )
已知:如图,l1∥l2∥l3,则在下列比例中一定成立的是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、口袋中装有2个红球和1个白球,从中摸出2个球,其中必有红球 |
| B、“如果a,b是实数,那么a+b=b+a”是不确定事件 |
| C、为了了解一批炮弹的杀伤力,采用普查的方式比较合适 |
| D、两个相似图形一定是位似图形 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com